When I was a lad in the 1960's, I became fascinated with the "new math" of nodes and lines known as "Network Analysis."
I always wondered whatever happened to it. Well, I wonder no more!
Apparently it changed its name to Graph Theory, and since my main hobby is Quantum Gravity, that reminded me of
Fotini Markopoulou-Kalamara's Quantum Graphity.
So, what is that? It's this (from 2 Wiki articles):
In
mathematics, a
random graph is a
graph that is generated by some
random process.
[1] The theory of random graphs lies at the intersection between
graph theory and
probability theory, and studies the properties of typical random graphs.
Random graph models
A random graph is obtained by starting with a set of
n vertices and adding edges between them at random. Different
random graph models produce different
probability distributions on graphs. Most commonly studied is the one proposed by
Edgar Gilbert, denoted
G(n,p), in which every possible edge occurs independently with probability
p. A closely related model, the
Erdős–Rényi model denoted
G(n,M), assigns equal probability to all graphs with exactly
M edges. The latter model can be viewed as a snapshot at a particular time (
M) of the
random graph process 
, which is a
stochastic process that starts with
n vertices and no edges, and at each step adds one new edge chosen uniformly from the set of missing edges.
If instead we start with an infinite set of vertices, and again let every possible edge occur independently with probability
p, then we get an object
G called an
infinite random graph. Except in the trivial cases when
p is 0 or 1, such a
G almost surely has the following property:
- Given any n + m elements
 , there is a vertex
, there is a vertex  that is adjacent to each of
that is adjacent to each of 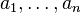 and is not adjacent to any of
and is not adjacent to any of  .
.
It turns out that if the vertex set is
countable then there is,
up to isomorphism, only a single graph with this property, namely the
Rado graph. Thus any countably infinite random graph is almost surely the Rado graph, which for this reason is sometimes called simply the
random graph. However, the analogous result is not true for uncountable graphs, of which there are many (nonisomorphic) graphs satisfying the above property.
Another model, which generalizes Gilbert's random graph model, is the
random dot-product model. A random dot-product graph associates with each vertex a
real vector. The probability of an edge
uv between any vertices
u and
v is some function of the
dot product u •
v of their respective vectors.
The
network probability matrix models random graphs through edge probabilities, which represent the probability
pi,j that a given edge
ei,j exists for a specified time period. This model is extensible to directed and undirected; weighted and unweighted; and static or dynamic graphs.
For
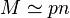
the two most widely used models,
G(n,M) and
G(n,p), are almost interchangeable
[2].
Random regular graphs form a special case, with properties that may differ from random graphs in general.
Properties of random graphs
The theory of random graphs studies typical properties of random graphs, those that hold with high probability for graphs drawn from a particular distribution. For example, we might ask for a given value of
n and
p what the probability is that
G(n,p) is
connected. In studying such questions, researchers often concentrate on the asymptotic behavior of random graphs—the values that various probabilities converge to as
n grows very large.
Percolation theory characterizes the connectedness of random graphs, especially infinitely large ones.
(threshold functions, evolution of G~)
Random graphs are widely used in the
probabilistic method, where one tries to prove the existence of graphs with certain properties. The existence of a property on a random graph can often imply, via the famous
Szemerédi regularity lemma, the existence of that property on almost all graphs.
Random trees
Main article:
random treeA
random tree is a
tree or
arborescence that is formed by a
stochastic process. Types of random trees include
uniform spanning tree,
random minimal spanning tree,
random binary tree,
treap,
rapidly-exploring random tree,
Brownian tree, and
random forest.
History
Random graphs were first defined by
Paul Erdős and
Alfréd Rényi in their 1959 paper "On Random Graphs"
[3] and independently by Gilbert in his paper "Random graphs"
[4].
See also
The term
event symmetry refers to invariance principles that have been used in some discrete approaches to
quantum gravity where the
diffeomorphism invariance of
general relativity can be extended to a
covariance under any permutation of spacetime events.
[1]
The principle of event symmetry
What it means
Since general relativity was discovered by
Albert Einstein in 1915 it has been demonstrated by observation and experiment to be an accurate theory of gravitation up to cosmic scales. On small scales the laws of
quantum mechanics have likewise been found to describe nature in a way consistent with every experiment performed, so far. To describe the laws of the universe fully a synthesis of general relativity and quantum mechanics must be found. Only then can physicists hope to understand the realms where both gravity and quantum come together. The
big bang is one such place.
The task to find such a theory of quantum gravity is one of the major scientific endeavours of our time. Many physicists believe that
string theory is the leading candidate, but string theory has so far failed to provide an adequate description of the big bang, and its success is just as incomplete in other ways. That could be because physicists do not really know what the correct underlying principles of string theory are, so they do not have the right formulation that would allow them to answer the important questions. In particular, string theory treats
spacetime in quite an old fashioned way even though it indicates that spacetime must be very different at small scales from what we are familiar with.
General relativity by contrast, is a model theory based on a geometric symmetry principle from which its dynamics can be elegantly derived. The symmetry is called
general covariance or
diffeomorphism invariance. It says that the dynamical equations of the gravitational field and any matter must be unchanged in form under any smooth transformation of spacetime coordinates. To understand what that means you have to think of a region of spacetime as a set of
events, each one labelled by unique values of four coordinate values x,y,z, and t. The first three tell us
where in space the event happened, while the fourth is time and tells us
when it happened. But the choice of coordinates that are used is arbitrary, so the laws of physics should not depend on what the choice is. It follows that if any smooth mathematical function is used to map one coordinate system to any other, the equations of dynamics must transform in such a way that they look the same as they did before. This symmetry principle is a strong constraint on the possible range of equations and can be used to derive the laws of gravity almost uniquely.
The principle of general covariance works on the assumption that spacetime is smooth and continuous. Although this fits in with our normal experience, there are reasons to suspect that it may not be a suitable assumption for quantum gravity. In quantum field theory, continuous fields are replaced with a more complex structure that has a dual particle-wave nature as if they can be both continuous and discrete depending on how you measure them. Research in string theory and several other approaches to quantum gravity suggest that spacetime must also have a dual continuous and discrete nature, but without the power to probe spacetime at sufficient energies it is difficult to measure its properties directly to find out how such a quantised spacetime should work.
This is where event symmetry comes in. In a discrete spacetime treated as a disordered set of events it is natural to extend the symmetry of general covariance to a discrete event symmetry in which any function mapping the set of events to itself replaces the smooth functions used in general relativity. Such a function is also called a
permutation, so the principle of event symmetry states that the equations governing the laws of physics must be unchanged when transformed by any permutation of spacetime events.
How it works
It is not immediately obvious how event symmetry could work. It seems to say that taking one part of space time and swapping it with another part a long distance away is a valid physical operation and that the laws of physics have to be written in such a way that this is supported. Clearly this symmetry can only be correct if it is hidden or broken. To get this in perspective consider what the symmetry of general relativity seems to say.
A smooth coordinate transformation or diffeomorphism can stretch and twist spacetime in any way so long as it is not torn. The laws of general relativity are unchanged in form under such a transformation. Yet this does not mean that objects can be stretched or bent without being opposed by a physical force. Likewise, event symmetry does not mean that objects can be torn apart in the way the permutations of spacetime would make us believe. In the case of general relativity the gravitational force acts as a background field that controls the measurement properties of spacetime. In ordinary circumstances the geometry of space is flat and Euclidean and the diffeomorphism invariance of general relativity is hidden thanks to this background field. Only in the extreme proximity of a violent collision of
black holes would the flexibility of spacetime become apparent. In a similar way, event symmetry could be hidden by a background field that determines not just the geometry of spacetime, but also its topology.
General relativity is often explained in terms of curved spacetime. We can picture the universe as the curved surface of a membrane like a soap film which changes dynamically in time. The same picture can help us understand how event symmetry would be broken. A soap bubble is made from molecules which interact via forces that depend on the orientations of the molecules and the distance between them. If you wrote down the equations of motion for all the molecules in terms of their positions, velocities and orientations, then those equations would be unchanged in form under any permutation of the molecules (which we will assume to be all the same). This is mathematically analogous to the event symmetry of spacetime events. The equations may be different, and unlike the molecules on the surface of a bubble, the events of spacetime are not embedded in a higher dimensional space, yet the mathematical principle is the same.
Physicists do not presently know if event symmetry is a correct symmetry of nature, but the example of a
soap bubble shows that it is a logical possibility. If it can be used to explain real physical observations then it merits serious consideration.
Maximal Permutability
American philosopher of physics
John Stachel has used permutability of spacetime events to generalize Einstein's
hole argument[2]. Statchel uses the term
quiddity to describe the universal qualities of an entity and
haecceity to describe its individuality. He makes use of the analogy with quantum mechanical particles, that have quiddity but no haecceity. The permutation symmetry of systems of particles leaves the equations of motion and the description of the system invariant. This is generalised to a
principle of maximal permutability[3] that should be applied to physical entities. In an approach to quantum gravity where spacetime events are discrete, the principle implies that physics must be symmetric under any permutations of events, so the principle of event symmetry is a special case of the principle of maximal permutability.
Stachel's view builds on the work of philosophers such as
Gottfried Leibniz whose
monadology proposed that the world should be viewed only in terms of relations between objects rather than their absolute positions.
Ernst Mach used this to formulate his relational principle which influenced Einstein in his formulation of general relativity. Some quantum gravity physicists believe that the true theory of quantum gravity will be a
relational theory with no spacetime. The events of spacetime are then no longer a background in which physics happens. Instead they are just the set of events where an interaction between entities took place. Characteristics of spacetime that we are familiar with (such as distance, continuity and dimension) should be
emergent in such a theory, rather than put in by hand.
Quantum Graphity and other random graph models
In a
random graph model of spacetime, points in space or events in spacetime are represented by nodes of a graph. Each node may be connected to any other node by a link. In mathematical terms this structure is called a graph. The smallest number of links that it takes to go between two nodes of the graph can be interpreted as a measure of the distance between them in space. The dynamics can be represented either by using a
Hamiltonian[disambiguation needed] formalism if the nodes are points in space, or a
Lagrangian formalism if the nodes are events in spacetime. Either way, the dynamics allow the links to connect or disconnect in a random way according to specified probability rule. The model is event-symmetric if the rules are invariant under any permutation of the graph nodes.
The mathematical discipline of
random graph theory was founded in the 1950s by
Paul Erdős and
Alfréd Rényi [4]. They proved the existence of sudden changes in characteristics of a random graph as parameters of the model varied. These are similar to phase transitions in physical systems. The subject has been extensively studied since with applications in many areas including computation and biology. A standard text is "Random Graphs" by
Béla Bollobás[5].
Application to quantum gravity came later. Early random graph models of space-time have been proposed by Frank Antonsen (1993)
[6], Manfred Requardt (1996)
[7] and Thomas Filk (2000)
[8]. Tomasz Konopka,
Fotini Markopoulou-Kalamara,
Simone Severini and
Lee Smolin of the Canadian
Perimeter Institute for Theoretical Physics introduced a graph model that they called
Quantum Graphity[9],
[10][11] . An argument based on quantum graphity combined with the
holographic principle can resolve the
horizon problem and explain the observed
scale invariance of
cosmic background radiation fluctuations without the need for
cosmic inflation[12].
In the quantum graphity model, points in spacetime are represented by nodes on a graph connected by links that can be
on or
off. This indicates whether or not the two points are directly connected as if they are next to each other in spacetime. When they are
on the links have additional state variables which are used to define the random dynamics of the graph under the influence of quantum fluctuations and temperature. At high temperature the graph is in
Phase I where all the points are randomly connected to each other and no concept of spacetime as we know it exists. As the temperature drops and the graph cools, it is conjectured to undergo a phase transition to a
Phase II where spacetime forms. It will then look like a spacetime manifold on large scales with only near-neighbour points being connected in the graph. The hypothesis of quantum graphity is that this
geometrogenesis models the condensation of spacetime in the
big bang.
Event symmetry and string theory
String theory is formulated on a background spacetime just as quantum field theory is. Such a background fixes spacetime curvature which in general relativity is like saying that the gravitational field is fixed. However, analysis shows that the excitations of the string fields act as
gravitons which can perturb the gravitational field away from the fixed background, so string theory is actually a theory which includes dynamic quantised gravity. More detailed studies have shown that different string theories in different background spacetimes can be related by dualities. There is also good evidence that string theory supports changes in topology of spacetime. Relativists have therefore criticised string theory for not being formulated in a background independent way, so that changes of spacetime geometry and topology can be more directly expressed in terms of the fundamental degrees of freedom of the strings.
The difficulty in achieving a truly background independent formulation for
string theory is demonstrated by a problem known as Witten's Puzzle
[13].
Ed Witten asked the question "What could the full symmetry group of string theory be if it includes diffeomorphism invariance on a spacetime with changing topology?". This is hard to answer because the diffeomorphism group for each spacetime topology is different and there is no natural way to form a larger group containing them all such that the action of the group on continuous spacetime events makes sense. This puzzle is solved if the spacetime is regarded as a discrete set of events with different topologies formed dynamically as different string field configurations. Then the full symmetry need only contain the permutation group of spacetime events. Since any diffeomorphism for any topology is a special kind of permutation on the discrete events, the permutation group does contain all the different diffeomorphism groups for all possible topologies.
There is some evidence from Matrix Models that event-symmetry is included in string theory. A random matrix model can be formed from a random graph model by taking the variables on the links of the graph and arranging them in a N by N square matrix, where N is the number of nodes on the graph. The element of the matrix in the n
th column and m
th row gives the variable on the link joining the n
th nodes to the m
th node. The event-symmetry can then be extended to a larger N dimensional rotational symmetry.
In string theory,
random matrix models were introduced to provide a non-perturbative formulation of
M-Theory using
noncommutative geometry. Coordinates of spacetime are normally
commutative but in noncommutative geometry they are replaced by matrix operators that do not commute. In the original M(atrix) Theory these matrices were interpreted as connections between
instantons (also known as D0-branes), and the matrix rotations were a gauge symmetry. Later, Iso and Kawai reinterpreted this as a permutation symmetry of space-time events
[14] and argued that diffeomorphism invariance was included in this symmetry. The two interpretations are equivalent if no distinction is made between instantons and events, which is what would be expected in a relational theory. This shows that Event Symmetry can already be regarded as part of string theory.
Trivia
Greg Egan's Dust Theory
The first known publication of the idea of event symmetry is in a work of science fiction rather than a journal of science.
Greg Egan used the idea in a short story called "Dust" in 1992
[15] and expanded it into the novel
Permutation City in 1995. Egan used dust theory as a way of exploring the question of whether a perfect computer simulation of a person differs from the real thing. However, his description of the dust theory as an extension of general relativity is also a consistent statement of the principle of event symmetry as used in quantum gravity.
The essence of the argument can be found in chapter 12 of "Permutation City". Paul, the main character of the story set in the future, has created a copy of himself in a computer simulator. The simulation runs on a distributed network which is sufficiently powerful to emulate his thoughts and experiences. Paul argues that the events of his simulated world have been remapped to events in the real world by the computer in a way that resembles a coordinate transformation in relativity. General relativity only allows for covariance under continuous transformations whereas the computer network has formed a discontinuous mapping which permutes events like "a cosmic anagram". Yet Paul's copy in the simulator experiences physics as if it was unchanged. Paul realises that this is "Like […] gravity and acceleration in General Relativity — it all depends on what you can't tell apart. This is a new Principle of Equivalence, a new symmetry between observers."







 , which is a
, which is a  , there is a vertex
, there is a vertex  that is adjacent to each of
that is adjacent to each of 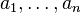 and is not adjacent to any of
and is not adjacent to any of  .
.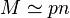 the two most widely used models, G(n,M) and G(n,p), are almost interchangeable
the two most widely used models, G(n,M) and G(n,p), are almost interchangeable



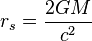








![\bar{a} = -2d_1 \left( \bar{ \omega} \times \bar v \right) - d_2 \left[ \bar{ \omega} \times \left( \bar{ \omega} \times \bar{r} \right) + 2\left( \bar{ \omega}\bar{r} \right) \bar{ \omega} \right]](http://upload.wikimedia.org/math/9/8/c/98c371696910069c25f914790a842201.png)