Friday, October 8, 2010

Carl Gauss


Johann Carl Friedrich Gauss (pronounced /ˈɡaʊs/; German: Gauß About this sound listen (help·info), Latin: Carolus Fridericus Gauss) (30 April 1777 – 23 February 1855) was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.

Sometimes referred to as the Princeps mathematicorum[1] (Latin, "the Prince of Mathematicians" or "the foremost of mathematicians") and "greatest mathematician since antiquity," Gauss had a remarkable influence in many fields of mathematics and science and is ranked as one of history's most influential mathematicians.[2] He referred to mathematics as "the queen of sciences."[3]

Gauss was a child prodigy. There are many anecdotes pertaining to his precocity while a toddler, and he made his first ground-breaking mathematical discoveries while still a teenager. He completed Disquisitiones Arithmeticae, his magnum opus, in 1798 at the age of 21, though it was not published until 1801. This work was fundamental in consolidating number theory as a discipline and has shaped the field to the present day.

Contents

[hide]

Early years (1777–1798)

Statue of Gauss at his birthplace, Braunschweig

Carl Friedrich Gauss was born on April 30, 1777 in Braunschweig, in the Electorate of Brunswick-Lüneburg, now part of Lower Saxony, Germany, as the son of poor working-class parents.[4] He was christened and confirmed in a church near the school he attended as a child.[5] There are several stories of his early genius. According to one, his gifts became very apparent at the age of three when he corrected, mentally and without fault in his calculations, an error his father had made on paper while calculating finances.

Another famous story has it that in primary school after the young Gauss misbehaved, his teacher, J.G. Büttner, gave him a task : add a list of integers in arithmetic progression; as the story is most often told, these were the numbers from 1 to 100. The young Gauss reputedly produced the correct answer within seconds, to the astonishment of his teacher and his assistant Martin Bartels.

Gauss's presumed method was to realize that pairwise addition of terms from opposite ends of the list yielded identical intermediate sums: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, and so on, for a total sum of 50 × 101 = 5050. However, the details of the story are at best uncertain (see [6] for discussion of the original Wolfgang Sartorius von Waltershausen source and the changes in other versions); some authors, such as Joseph Rotman in his book A first course in Abstract Algebra, question whether it ever happened.

Gauss's intellectual abilities attracted the attention of the Duke of Braunschweig,[2] who sent him to the Collegium Carolinum (now Technische Universität Braunschweig), which he attended from 1792 to 1795, and to the University of Göttingen from 1795 to 1798. While in university, Gauss independently rediscovered several important theorems;[citation needed] his breakthrough occurred in 1796 when he was able to show that any regular polygon with a number of sides which is a Fermat prime (and, consequently, those polygons with any number of sides which is the product of distinct Fermat primes and a power of 2) can be constructed by compass and straightedge. This was a major discovery in an important field of mathematics; construction problems had occupied mathematicians since the days of the Ancient Greeks, and the discovery ultimately led Gauss to choose mathematics instead of philology as a career. Gauss was so pleased by this result that he requested that a regular heptadecagon be inscribed on his tombstone. The stonemason declined, stating that the difficult construction would essentially look like a circle.[7]

The year 1796 was most productive for both Gauss and number theory. He discovered a construction of the heptadecagon on March 30.[8] He invented modular arithmetic, greatly simplifying manipulations in number theory.[citation needed] He became the first to prove the quadratic reciprocity law on 8 April. This remarkably general law allows mathematicians to determine the solvability of any quadratic equation in modular arithmetic. The prime number theorem, conjectured on 31 May, gives a good understanding of how the prime numbers are distributed among the integers. Gauss also discovered that every positive integer is representable as a sum of at most three triangular numbers on 10 July and then jotted down in his diary the famous words, "Heureka! num = Δ + Δ + Δ." On October 1 he published a result on the number of solutions of polynomials with coefficients in finite fields, which ultimately led to the Weil conjectures 150 years later.

Middle years (1799–1830)

In his 1799 doctorate in absentia, A new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree, Gauss proved the fundamental theorem of algebra which states that every non-constant single-variable polynomial over the complex numbers has at least one root. Mathematicians including Jean le Rond d'Alembert had produced false proofs before him, and Gauss's dissertation contains a critique of d'Alembert's work. Ironically, by today's standard, Gauss's own attempt is not acceptable, owing to implicit use of the Jordan curve theorem. However, he subsequently produced three other proofs, the last one in 1849 being generally rigorous. His attempts clarified the concept of complex numbers considerably along the way.

Gauss also made important contributions to number theory with his 1801 book Disquisitiones Arithmeticae (Latin, Arithmetical Investigations), which, among things, introduced the symbol ≡ for congruence and used it in a clean presentation of modular arithmetic, had the first two proofs of the law of quadratic reciprocity, developed the theories of binary and ternary quadratic forms, stated the class number problem for them, and showed that a regular heptadecagon (17-sided polygon) can be constructed with straightedge and compass.

Title page of Gauss's Disquisitiones Arithmeticae

In that same year, Italian astronomer Giuseppe Piazzi discovered the dwarf planet Ceres, but could only watch it for a few days. Gauss predicted correctly the position at which it could be found again, and it was rediscovered by Franz Xaver von Zach on 31 December 1801 in Gotha, and one day later by Heinrich Olbers in Bremen.

Gauss's method involved determining a conic section in space, given one focus (the sun) and the conic's intersection with three given lines (lines of sight from the earth, which is itself moving on an ellipse, to the planet) and given the time it takes the planet to traverse the arcs determined by these lines (from which the lengths of the arcs can be calculated by Kepler's Second Law). This problem leads to an equation of the eighth degree, of which one solution, the Earth's orbit, is known. The solution sought is then separated from the remaining six based on physical conditions. In this work Gauss used comprehensive approximation methods which he created for that purpose.[9]

Zach noted that "without the intelligent work and calculations of Doctor Gauss we might not have found Ceres again." Though Gauss had been up to that point supported by the stipend from the Duke, he doubted the security of this arrangement, and also did not believe pure mathematics to be important enough to deserve support. Thus he sought a position in astronomy, and in 1807 was appointed Professor of Astronomy and Director of the astronomical observatory in Göttingen, a post he held for the remainder of his life.

The discovery of Ceres by Piazzi on 1 January 1801 led Gauss to his work on a theory of the motion of planetoids disturbed by large planets, eventually published in 1809 under the name Theoria motus corporum coelestium in sectionibus conicis solem ambientum (theory of motion of the celestial bodies moving in conic sections around the sun). Piazzi had only been able to track Ceres for a couple of months, following it for three degrees across the night sky. Then it disappeared temporarily behind the glare of the Sun. Several months later, when Ceres should have reappeared, Piazzi could not locate it: the mathematical tools of the time were not able to extrapolate a position from such a scant amount of data—three degrees represent less than 1% of the total orbit.

Gauss, who was 23 at the time, heard about the problem and tackled it. After three months of intense work, he predicted a position for Ceres in December 1801—just about a year after its first sighting—and this turned out to be accurate within a half-degree. In the process, he so streamlined the cumbersome mathematics of 18th century orbital prediction that his work—published a few years later as Theory of Celestial Movement—remains a cornerstone of astronomical computation.[citation needed] It introduced the Gaussian gravitational constant, and contained an influential treatment of the method of least squares, a procedure used in all sciences to this day to minimize the impact of measurement error. Gauss was able to prove the method in 1809 under the assumption of normally distributed errors (see Gauss–Markov theorem; see also Gaussian). The method had been described earlier by Adrien-Marie Legendre in 1805, but Gauss claimed that he had been using it since 1795.[citation needed]

Gauss' portrait published in Astronomische Nachrichten 1828

Gauss was a prodigious mental calculator. Reputedly, when asked how he had been able to predict the trajectory of Ceres with such accuracy he replied, "I used logarithms." The questioner then wanted to know how he had been able to look up so many numbers from the tables so quickly. "Look them up?" Gauss responded. "Who needs to look them up? I just calculate them in my head!"[citation needed]

In 1818 Gauss, putting his calculation skills to practical use, carried out a geodesic survey of the state of Hanover, linking up with previous Danish surveys. To aid in the survey, Gauss invented the heliotrope, an instrument that uses a mirror to reflect sunlight over great distances, to measure positions.

Gauss also claimed to have discovered the possibility of non-Euclidean geometries but never published it. This discovery was a major paradigm shift in mathematics, as it freed mathematicians from the mistaken belief that Euclid's axioms were the only way to make geometry consistent and non-contradictory. Research on these geometries led to, among other things, Einstein's theory of general relativity, which describes the universe as non-Euclidean. His friend Farkas Wolfgang Bolyai with whom Gauss had sworn "brotherhood and the banner of truth" as a student had tried in vain for many years to prove the parallel postulate from Euclid's other axioms of geometry. Bolyai's son, János Bolyai, discovered non-Euclidean geometry in 1829; his work was published in 1832. After seeing it, Gauss wrote to Farkas Bolyai: "To praise it would amount to praising myself. For the entire content of the work... coincides almost exactly with my own meditations which have occupied my mind for the past thirty or thirty-five years."

Four Gaussian distributions in statistics

This unproved statement put a strain on his relationship with János Bolyai (who thought that Gauss was "stealing" his idea), but it is now generally taken at face value.[citation needed] Letters by Gauss years before 1829 reveal him obscurely discussing the problem of parallel lines. Waldo Dunnington, a life-long student of Gauss, successfully proves in Gauss, Titan of Science that Gauss was in fact in full possession of non-Euclidian geometry long before it was published by János Bolyai, but that he refused to publish any of it because of his fear of controversy.

The survey of Hanover fueled Gauss's interest in differential geometry, a field of mathematics dealing with curves and surfaces. Among other things he came up with the notion of Gaussian curvature. This led in 1828 to an important theorem, the Theorema Egregium (remarkable theorem in Latin), establishing an important property of the notion of curvature. Informally, the theorem says that the curvature of a surface can be determined entirely by measuring angles and distances on the surface. That is, curvature does not depend on how the surface might be embedded in 3-dimensional space or 2-dimensional space.

In 1821, he was made a foreign member of the Royal Swedish Academy of Sciences.

Later years and death (1831–1855)

Daguerreotype of Gauss on his deathbead, 1855.
Grave of Gauss at Albanifriedhof in Göttingen, Germany.

In 1831 Gauss developed a fruitful collaboration with the physics professor Wilhelm Weber, leading to new knowledge in magnetism (including finding a representation for the unit of magnetism in terms of mass, length and time) and the discovery of Kirchhoff's circuit laws in electricity. They constructed the first electromechanical telegraph in 1833, which connected the observatory with the institute for physics in Göttingen. Gauss ordered a magnetic observatory to be built in the garden of the observatory, and with Weber founded the magnetischer Verein (magnetic club in German), which supported measurements of earth's magnetic field in many regions of the world. He developed a method of measuring the horizontal intensity of the magnetic field which has been in use well into the second half of the 20th century and worked out the mathematical theory for separating the inner (core and crust) and outer (magnetospheric) sources of Earth's magnetic field.

Gauss died in Göttingen, Hannover (now part of Lower Saxony, Germany) in 1855 and is interred in the cemetery Albanifriedhof there. Two individuals gave eulogies at his funeral, Gauss's son-in-law Heinrich Ewald and Wolfgang Sartorius von Waltershausen, who was Gauss's close friend and biographer. His brain was preserved and was studied by Rudolf Wagner who found its mass to be 1,492 grams and the cerebral area equal to 219,588 square millimeters[10] (340.362 square inches). Highly developed convolutions were also found, which in the early 20th century was suggested as the explanation of his genius.[2]

Religion

Wiki letter w.svg This section requires expansion.

According to Dunnington, Gauss's religion was based upon the search for truth. He believed in "the immortality of the spiritual individuality, in a personal permanence after death, in a last order of things, in an eternal, righteous, omniscient and omnipotent God." Gauss also upheld religious tolerance, believing it wrong to disturb others who were at peace with their own beliefs.[2]

Family

Gauss' daughter Therese (1816—1864)

Gauss's personal life was overshadowed by the early death of his first wife, Johanna Osthoff, in 1809, soon followed by the death of one child, Louis. Gauss plunged into a depression from which he never fully recovered. He married again, to Johanna's best friend named Friederica Wilhelmine Waldeck but commonly known as Minna. When his second wife died in 1831 after a long illness,[11] one of his daughters, Therese, took over the household and cared for Gauss until the end of his life. His mother lived in his house from 1817 until her death in 1839.[2]

Gauss had six children. With Johanna (1780–1809), his children were Joseph (1806–1873), Wilhelmina (1808–1846) and Louis (1809–1810). Of all of Gauss's children, Wilhelmina was said to have come closest to his talent, but she died young. With Minna Waldeck he also had three children: Eugene (1811–1896), Wilhelm (1813–1879) and Therese (1816–1864). Eugene emigrated to the United States about 1832 after a falling out with his father.[citation needed] Wilhelm also settled in Missouri, starting as a farmer and later becoming wealthy in the shoe business in St. Louis. Therese kept house for Gauss until his death, after which she married.

Gauss eventually had conflicts with his sons, two of whom migrated to the United States. He did not want any of his sons to enter mathematics or science for "fear of sullying the family name".[citation needed] Gauss wanted Eugene to become a lawyer, but Eugene wanted to study languages. They had an argument over a party Eugene held, which Gauss refused to pay for. The son left in anger and emigrated to the United States, where he was quite successful. It took many years for Eugene's success to counteract his reputation among Gauss's friends and colleagues. See also the letter from Robert Gauss to Felix Klein on 3 September 1912.

Personality

Gauss was an ardent perfectionist and a hard worker. According to Isaac Asimov, Gauss was once interrupted in the middle of a problem and told that his wife was dying. He is purported to have said, "Tell her to wait a moment till I'm done."[12] This anecdote is briefly discussed in G. Waldo Dunnington's Gauss, Titan of Science where it is suggested that it is an apocryphal story.

He was never a prolific writer, refusing to publish work which he did not consider complete and above criticism. This was in keeping with his personal motto pauca sed matura ("few, but ripe"). His personal diaries indicate that he had made several important mathematical discoveries years or decades before his contemporaries published them. Mathematical historian Eric Temple Bell estimated that had Gauss timely published all of his discoveries, Gauss would have advanced mathematics by fifty years.[13]

Though he did take in a few students, Gauss was known to dislike teaching. It is said that he attended only a single scientific conference, which was in Berlin in 1828. However, several of his students became influential mathematicians, among them Richard Dedekind, Bernhard Riemann, and Friedrich Bessel. Before she died, Sophie Germain was recommended by Gauss to receive her honorary degree.

Gauss usually declined to present the intuition behind his often very elegant proofs—he preferred them to appear "out of thin air" and erased all traces of how he discovered them.[citation needed] This is justified, if unsatisfactorily, by Gauss in his "Disquisitiones Arithmeticae", where he states that all analysis (i.e. the paths one travelled to reach the solution of a problem) must be suppressed for sake of brevity.

Gauss supported monarchy and opposed Napoleon, whom he saw as an outgrowth of revolution.

Commemorations

A 10 Deutsche Mark banknote from Germany 1993 (discontinued) showing Gauss
Gauss (about 26) on an East-German stamp produced in 1977. Heptadecagon, compass and straightedge are shown next to him.

From 1989 until the end of 2001, his portrait and a normal distribution curve as well as some prominent buildings of Göttingen were featured on the German ten-mark banknote. The other side of the note features the heliotrope and a triangulation approach for Hannover. Germany has issued three stamps honouring Gauss, as well. A righteous stamp (no. 725), was issued in 1955 on the hundredth anniversary of his death; two other stamps, no. 1246 and 1811, were issued in 1977, the 200th anniversary of his birth.

Daniel Kehlmann's 2005 novel Die Vermessung der Welt, translated into English as Measuring the World: a Novel in 2006, explores Gauss's life and work through a lens of historical fiction, contrasting it with the German explorer Alexander von Humboldt.

In 2007, his bust was introduced to the Walhalla temple.[14]

Things named in honour of Gauss include:

Writings

  • 1799: Doctoral dissertation on the Fundamental theorem of algebra, with the title: Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse ("New proof of the theorem that every integral algebraic function of one variable can be resolved into real factors [i.e. polynomials] of the first or second degree")
  • 1801: Disquisitiones Arithmeticae. German translation by H. Maser Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). New York: Chelsea. 1965. ISBN 0-8284-0191-8 , pp. 1–453. English translation by Arthur A. Clarke Disquisitiones Arithemeticae (Second, corrected edition). New York: Springer. 1986. ISBN 0387962549 .
  • 1808: Theorematis arithmetici demonstratio nova. Göttingen: Comment. Soc. regiae sci, Göttingen XVI . German translation by H. Maser Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). New York: Chelsea. 1965. ISBN 0-8284-0191-8 , pp. 457–462 [Introduces Gauss's lemma, uses it in the third proof of quadratic reciprocity]
  • 1811: Summatio serierun quarundam singularium. Göttingen: Comment. Soc. regiae sci, Göttingen . German translation by H. Maser Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). New York: Chelsea. 1965. ISBN 0-8284-0191-8 , pp. 463–495 [Determination of the sign of the quadratic Gauss sum, uses this to give the fourth proof of quadratic reciprocity]
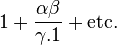
  • 1812: Disquisitiones Generales Circa Seriem Infinitam 1+\frac{\alpha\beta}{\gamma.1}+\mbox{etc.}
  • 1818: Theorematis fundamentallis in doctrina de residuis quadraticis demonstrationes et amplicationes novae. Göttingen: Comment. Soc. regiae sci, Göttingen . German translation by H. Maser Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). New York: Chelsea. 1965. ISBN 0-8284-0191-8 , pp. 496–510 [Fifth and sixth proofs of quadratic reciprocity]
  • 1821, 1823 und 1826: Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend die Wahrscheinlichkeitsrechnung als Grundlage des Gauß'schen Fehlerfortpflanzungsgesetzes. English translation by G. W. Stewart, 1987, Society for Industrial Mathematics.
  • 1828: Theoria residuorum biquadraticorum, Commentatio prima. Göttingen: Comment. Soc. regiae sci, Göttingen 6 . German translation by H. Maser Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). New York: Chelsea. 1965. ISBN 0-8284-0191-8 , pp. 511–533 [Elementary facts about biquadratic residues, proves one of the supplements of the law of biquadratic reciprocity (the biquadratic character of 2)]
  • 1832: Theoria residuorum biquadraticorum, Commentatio secunda. Göttingen: Comment. Soc. regiae sci, Göttingen 7 . German translation by H. Maser Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition). New York: Chelsea. 1965. ISBN 0-8284-0191-8 , pp. 534–586 [Introduces the Gaussian integers, states (without proof) the law of biquadratic reciprocity, proves the supplementary law for 1 + i]
  • Mathematisches Tagebuch 1796–1814, Ostwaldts Klassiker, Harri Deutsch Verlag 2005, mit Anmerkungen von Neumamn, ISBN 978-3-8171-3402-1 (English translation with annotations by Jeremy Gray: Expositiones Math. 1984)
  • Gauss' collective works are online here This includes German translations of Latin texts and commentaries by various authorities

See also

Notes

  1. ^ Zeidler, Eberhard (2004). Oxford User's Guide to Mathematics. Oxford, UK: Oxford University Press. p. 1188. ISBN 0198507631.
  2. ^ a b c d e Dunnington, G. Waldo. (May, 1927). "The Sesquicentennial of the Birth of Gauss". Scientific Monthly XXIV: 402–414. Retrieved on 29 June 2005. Comprehensive biographical article.
  3. ^ Smith, S. A., et al. 2001. Algebra 1: California Edition. Prentice Hall, New Jersey. ISBN 0130442631
  4. ^ "Carl Friedrich Gauss". Wichita State University. http://www.math.wichita.edu/history/men/gauss.html.
  5. ^ Susan Chambless. "Author — Date". Homepages.rootsweb.ancestry.com. http://homepages.rootsweb.ancestry.com/~schmblss/home/Letters/Gauss/1911-07-26b.htm. Retrieved 2009-07-19.
  6. ^ http://www.americanscientist.org/issues/pub/gausss-day-of-reckoning/2
  7. ^ Pappas, Theoni: Mathematical Snippets, Page 42. Pgw 2008
  8. ^ Carl Friedrich Gauss §§365–366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. New Haven, CT: Yale University Press, 1965.
  9. ^ Klein, Felix; Hermann, Robert (1979). Development of mathematics in the 19th century. Math Sci Press. ISBN 9780915692286.
  10. ^ This reference from 1891 (Donaldson, Henry H. (1891). "Anatomical Observations on the Brain and Several Sense-Organs of the Blind Deaf-Mute, Laura Dewey Bridgman". The American Journal of Psychology (E. C. Sanford) 4 (2): 248–294. doi:10.2307/1411270. http://jstor.org/stable/1411270. ) says: "Gauss, 1492 grm. 957 grm. 219588. sq. mm. ", i.e the unit is square mm. In the later reference: Dunnington (1927), the unit is erroneously reported as square cm, which gives an unreasonably large area, the 1891 reference is more reliable.
  11. ^ "Gauss biography". Groups.dcs.st-and.ac.uk. http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Gauss.html. Retrieved 2008-09-01.
  12. ^ Asimov, I. (1972). Biographical Encyclopedia of Science and Technology; the Lives and Achievements of 1195 Great Scientists from Ancient Times to the Present, Chronologically Arranged.. New York: Doubleday.
  13. ^ Bell, E. T. (2009). "Ch. 14: The Prince of Mathematicians: Gauss". Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincaré. New York: Simon and Schuster. pp. 218–269. ISBN 0-671-46400-0.
  14. ^ "Bayerisches Staatsministerium für Wissenschaft, Forschung und Kunst: Startseite". Stmwfk.bayern.de. http://www.stmwfk.bayern.de/downloads/aviso/2004_1_aviso_48-49.pdf. Retrieved 2009-07-19.
  15. ^ Andersson, L. E.; Whitaker, E. A., (1982). NASA Catalogue of Lunar Nomenclature. NASA RP-1097.

Further reading

External links

at

No comments:

Post a Comment