That's from a website called Mathematical Imagery by Jos Leys. No, I don't know how I found that. Internet surfing lands us in the strangest places. :-)
KLEIN BOTTLE MATHS (for those who like Maths, and beware, this is about your run-of-the-mill Klein bottle, not the .... thing in the photograph above ...... ) :
The "figure 8" immersion (Klein bagel) of the Klein bottle has a particularly simple parameterization. It is that of a "figure-8" torus with a 180 degree "Möbius" twist inserted:
The parameterization of the 3-dimensional immersion of the bottle itself is much more complicated. Here is a simplified version:
In this parameterization, u follows the length of the bottle's body while v goes around its circumference.
UM-m-m, OK.
Off topic: This webpage (The Best NYC Pastrami Sandwich restaurants) is wrong. The best hot-pastrami-on-rye sandwich on Earth can be found at Harold's New York Deli Restaurant in Edison, New Jersey. ;-p
Important note: Like the website says, all in CAPS, sorry: HAROLD JAFFE, OWNER OF HAROLD'S NY DELI IN EDISON NEW JERSEY IS NOT IN ANY WAY AFFILIATED WITH
HAROLD'S DELI IN PARSIPPANY NJ OR ANY OTHER LOCATION
Trust me, he's not kidding, cuz I've eaten at both. Go to Edison, or don't go at all. The Parsippany Pastrami ain't bad, but it ain't as good as Jaffe's restaurant in Edison, unless "average" or "OK" turns you on. IMO, which I'm entitled to.

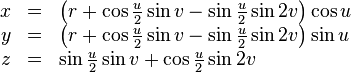
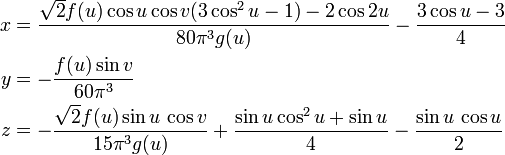
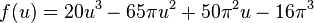

Steve,
ReplyDeleteIt looks like the recycling logo for the 21st century... way cool...
off topic, I'm thinking there must be some kind of intellectual game where you make a word or acronym out of the word verification things on comment pages and such. A hit tv show in the waiting?
You mean like that old military word: FUBAR ?
ReplyDeleteFUBAR = Frequently Underachieving Ballistic Arms Reduction
Sure that's what it means (smirks).
Oh, I have a MUCH better Mathematical artwork on the way. Or, um, AS good, because God forgive us we compare artworks, beauty being in the eye of the of the beholder and whatnot. :-)
Interesting Article. Hoping that you will continue posting an article having a useful information. American Music Drama Academy
ReplyDeleteIt is a very informative and useful post thanks it is good material to read this post increases my knowledge. Chicwish
ReplyDelete