The Mach–Zehnder interferometer is a device used to determine the relative phase shift between two collimated beams from acoherent light source. The interferometer has been used, amongst other things, to measure small phase shifts in one of the two beams caused by a small sample or the change in length of one of the paths. The apparatus is named after the physicists Ludwig Mach (the son of Ernst Mach) and Ludwig Zehnder.
The Michelson interferometer is a Mach–Zehnder interferometer that has been folded back upon itself. The principal difference is that in the Michelson interferometer, the beam splitting optic is also used to recombine the beams.
Contents |
How it works
Set-up
A collimated beam is split by a half-silvered mirror. The two resulting beams (the "sample beam" and the "reference beam") are each reflected by a mirror. The two beams then pass a second half-silvered mirror and enter two detectors ("detector 1" and "detector 2"). It is important that the fully-silvered and half-silvered surfaces of all mirrors, except the last, face the inbound beam, and that the half-silvered surface of the last mirror faces the outbound beam exiting in the same orientation as the original collimated beam. That is, if the original beam is horizontal, the half-silvered surface of the last mirror should face the horizontally outbound beam.
Properties
It is important to consider that the medium of a mirror is what lies behind it; that is, if a glass substrate has its half-silvered or fully-silvered surface facing the inbound beam, then the inbound beam travels through air and is reflected off the surface of a glass medium. If, however, the half-silvered or fully-silvered surface faces away from the inbound beam, then the inbound beam travels through glass and is reflecting off the surface of an air medium.
The following rules apply to phase shifts due to material:
- Reflection or refraction at the surface of a medium with a lower refractive index causes no phase shift.
- Reflection at the surface of a medium with a higher refractive index causes a phase shift of half of awavelength.
- The speed of light is slower in media with an index of refraction greater than that of a vacuum, which is 1. Specifically, its speed is:
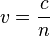, where c is the speed of light in vacuum and n is the index of refraction. This causes a phase shift increase proportional to (n − 1) × length traveled.
Given the above rules, mirrors, including half-silvered mirrors, have the following properties:
- A ½ wavelength phase shift occurs upon reflection from the front of a mirror, since the medium behind the mirror (glass) has a higher refractive index than the medium the light is traveling in (air).
- If k is the constant phase shift incurred by passing through a glass plate on which a mirror resides, a total of 2kphase shift occurs when reflecting off the rear of a mirror. This is because light traveling toward the rear of a mirror will enter the glass plate, incurring k phase shift, and then reflect off the mirror with no additional phase shift since only air is now behind the mirror, and travel again back through the glass plate incurring an additionalk phase shift.
Observing the effect of a sample
Without a sample, there is no phase difference in the two beams in detector 1, yielding constructive interference. Both beams will have undergone a phase shift of (wavelength + k) due to two front-side reflections and one transmission through a glass plate. At detector 2, there is a phase difference of half a wavelength, yielding complete destructive interference. The reference beam into detector 2 has undergone a phase shift of 0.5 ×(wavelength) + 2k due to one front-side reflection and two transmissions. The sample beam into detector 2 has undergone a (wavelength + 2k) phase shift due to two front-side reflections and one rear-side reflection. Therefore, when there is no sample, only detector 1 receives light.
If a sample is placed in the path of the sample beam, the intensities of the beams entering the two detectors will change, allowing the calculation of the phase shift caused by the sample.
See also
- Interferometer
- Elitzur–Vaidman bomb-tester
- Time-bin encoding
- Jamin interferometer
- Classical interference microscopy
- Dual polarisation interferometry
Flow visualisation techniques
References[
- Ludwig Zehnder, Z. Instrumentenkunde 11 (1891) 275.
- Ludwig Mach, Z. Instrumentenkunde 12 (1892) 89.
- Mach, Ernst (2003). The Principles of Physical Optics. Dover. ISBN 0-486-49559-0. p. 170. (First published in German in 1926.)
No comments:
Post a Comment