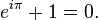Richard Feynman called Euler's formula "our jewel"
[2] and "one of the most remarkable, almost astounding, formulas in all of mathematics."
[3]
Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills by Paul J. Nahin, Professor Emeritus, University of New Hampshire, PhDEE
From
+ Plus magazine ... Living Mathematics Review by Lewis Dartnell
The hero of this book is Euler's formula:
eiπ + 1 = 0
This simple equation has been widely considered through the last two centuries to be one of the most beautiful formulae of mathematics, and Nahin tells us why.
The constant e is the base of the natural logarithm (and you might have used it in calculations on radioactive decay in physics lessons, for example), whereas &pi, as we all know, is the ratio of a circle's circumference to its diameter. Bothe and &pi are irrational numbers, that is, you could never write down all of their decimal places as they can be proven to continue for ever. The symbol i denotes the square root of -1, a value that does not even exist on the standard number line. Each of these three quantities is therefore curious in its own right, and they were originally developed within very different areas of maths. So how on Earth does ei&pi equal exactly -1? It seems like the biggest fluke in the Universe — and this is part the formula's exquisite beauty. It is also fairly easy to derive the formula yourself, and the proof can be found in any textbook on complex numbers. And as Nahin's book shows, it is also one of the most influential formulae in the history of mathematics.
The book starts off gently enough, with an Introduction leading the reader through a few examples of the most fundamental skill in mathematics; constructing a proof. We see, for example, why √2 must be irrational through a simple proof by contradiction. The process of proving things is mostly ignored at GCSE and A-level, but really does give an eye-opening insight into how real mathematics is often like solving a intriguing puzzle, rather than slogging through homework exercises to practice the basic skills.
Through the following six chapters of the book, Nahin shows us many of the applications of imaginary numbers, Euler's formula, and other mathematical formulae and techniques that have been built on this eighteenth century foundation, both in pure and applied maths. Regular Plusreaders might already know a little bit about some of these, and the sections in the book include: drawing regular prime number polygons, such as the 17-gon, using only a ruler and a compass; how to deconstruct any continuous function, such as a sound wave, into a set of sine waves — a technique that is crucial to modern gadgets like mp3 players. Nahin also shows us the maths of complex numbers lying behind the uncertainty principle of quantum mechanics, listening to the radio, and even how to build a telephone voice scrambler from simple electronics.
The book is well-written and illustrated with numerous diagrams and graphs. For those wanting a little more detail, or to follow up on the bibliography, the book is usefully cross-referenced and has hordes of end notes. But I do have one major warning for
Plus readers. Although this book is written to be more easy-reading and popularist than a text book, it is still very heavy-going. More importantly it is pitched at the level of university undergraduates. However, if you're enjoying maths A-level, then this book has a lot to offer, even if you don't understand everything. Every chapter begins with an interesting introduction on the history of a particular problem and the lives of the mathematicians involved, before heading into streams of equations and derivations. The final section of the book gives a detailed biography of the genius behind all of this mathematics through the ages,
Leonhard Euler. If you have a class project to write an essay on an influential mathematician, then Euler would certainly be an inspirational choice, and this final chapter a good place to start your research.
We will be discussing two equations. The ring illustrated above is Euler's Identity, which we will discuss second. Feynman's quote refers to Euler's formula, which we will discuss first. From Wikipedia:
Euler's formula, named after
Leonhard Euler, is a
mathematical formula in
complex analysis that establishes the deep relationship between the
trigonometric functions and the
complex exponential function. Euler's formula states that, for any
real number x,
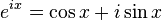
where
e is the
base of the natural logarithm,
i is the
imaginary unit, and cos and sin are the
trigonometric functions cosine and sine respectively, with the argument
x given in
radians. This complex exponential function is sometimes called
cis(
x). The formula is still valid if
x is a
complex number, and so some authors refer to the more general complex version as Euler's formula.
[1]
History
It was
Bernoulli [1702] who noted that

And since

the above equation tells us something about complex logarithms. Bernoulli, however, did not evaluate the integral. His correspondence with Euler (who also knew the above equation) shows that he didn't fully understand logarithms. Euler also suggested that the complex logarithms can have infinitely many values.
Meanwhile,
Roger Cotes, in 1714, discovered

(where "ln" means
natural logarithm, i.e. log with base
e).
[4] We now know that the above equation is only true
modulo integer multiples of
2πi, but Cotes missed the fact that a complex logarithm can have infinitely many values which owes to the periodicity of the trigonometric functions.
It was Euler (presumably around 1740) who turned his attention to the exponential function instead of logarithms, and obtained the correct formula now coined after his name. It was published in 1748, and his proof was based on the
infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the
complex plane arose only some 50 years later (see
Caspar Wessel).
Applications in complex number theory
This formula can be interpreted as saying that the function
eix traces out the
unit circle in the
complex number plane as
x ranges through the real numbers. Here,
x is the
angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in
radians.
The original proof is based on the
Taylor series expansions of the
exponential function ez (where
z is a complex number) and of sin
x and cos
x for real numbers
x (see below). In fact, the same proof shows that Euler's formula is even valid for all
complex numbers
z.
A point in the
complex plane can be represented by a complex number written in
cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and
polar coordinates. The polar form reduces the number of
terms from two to one, which simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number
z =
x +
iy can be written as


where
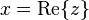 the real part
the real part the imaginary part
the imaginary part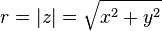 the magnitude of z
the magnitude of z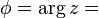 atan2(y, x) .
atan2(y, x) .

is the
argument of
z—i.e., the angle between the
x axis and the vector
z measured counterclockwise and in
radians—which is defined
up to addition of 2π. Many texts write tan
-1(
y/
x) instead of atan2(
y,
x) but this needs adjustment when
x ≤ 0.
Now, taking this derived formula, we can use Euler's formula to define the
logarithm of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation) that
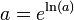
and that

both valid for any complex numbers
a and
b.
Therefore, one can write:

for any
z ≠ 0. Taking the logarithm of both sides shows that:

and in fact this can be used as the definition for the
complex logarithm. The logarithm of a complex number is thus a
multi-valued function, because
φ is multi-valued.
Finally, the other exponential law

which can be seen to hold for all integers
k, together with Euler's formula, implies several
trigonometric identities as well as
de Moivre's formula.
Relationship to trigonometry
Euler's formula provides a powerful connection between
analysis and
trigonometry, and provides an interpretation of the sine and cosine functions as
weighted sums of the exponential function
:


The two equations above can be derived by adding or subtracting Euler's formulas
:
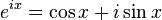
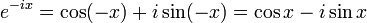
and solving for either cosine or sine.
These formulas can even serve as the definition of the trigonometric functions for complex arguments
x. For example, letting
x =
iy, we have
:
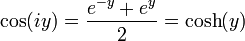

Complex exponentials can simplify trigonometry, because they are easier to manipulate than their sinusoidal components. One technique is simply to convert sinusoids into equivalent expressions in terms of exponentials.
After the manipulations, the simplified result is still real-valued. For example
:
![\begin{align}
\cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\
& = \frac{1}{2}\cdot \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2} \\
& = \frac{1}{2} \left[ \underbrace{ \frac{e^{i(x+y)} + e^{-i(x+y)}}{2} }_{\cos(x+y)} + \underbrace{ \frac{e^{i(x-y)} + e^{-i(x-y)}}{2} }_{\cos(x-y)} \right] \ .
\end{align}](http://upload.wikimedia.org/math/4/5/3/453afc84086fb72dbe8dc2bd17eed023.png)
Another technique is to represent the sinusoids in terms of the
real part of a more complex expression, and perform the manipulations on the complex expression. For example
:
![\begin{align}
\cos(nx) & = \mathrm{Re} \{\ e^{inx}\ \}
= \mathrm{Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot (e^{ix} + e^{-ix} - e^{-ix})\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot \underbrace{(e^{ix} + e^{-ix})}_{2\cos(x)} - e^{i(n-2)x}\ \} \\
& = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x] \ .
\end{align}](http://upload.wikimedia.org/math/a/7/e/a7e33560e9ae009ce7eb56b99babb19d.png)
This formula is used for recursive generation of cos(
nx) for integer values of
n and arbitrary
x (in radians).
Other applications
In
differential equations, the function
eix is often used to simplify derivations, even if the final answer is a real function involving sine and cosine. The reason for this is that the complex exponential is the
eigenfunction of differentiation.
Euler's identity is an easy consequence of Euler's formula.
In
electrical engineering and other fields, signals that vary periodically over time are often described as a combination of sine and cosine functions (see
Fourier analysis), and these are more conveniently expressed as the real part of exponential functions with
imaginary exponents, using Euler's formula. Also,
phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.
Definitions of complex exponentiation
The exponential function
ex for real values of
x may be defined in a few different equivalent ways (see
Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of
ez for complex values of
z simply by substituting
z in place of
x and using the complex algebraic operations. In particular we may use either of the two following definitions which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique
analytic continuation of
ex to the complex plane.
Power series definition
For complex
z
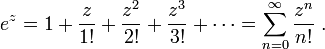
Using the
ratio test it is possible to show that this
power series has an infinite
radius of convergence, and so defines
ez for all complex
z.
Limit definition
For complex
z

Proofs
Various proofs of the formula are possible.
Using power series
Here is a proof of Euler's formula using power series expansions as well as basic facts about the powers of
i:

and so on. Using now the power series definition from above we see that for real values of
x
![\begin{align}
e^{ix} &{}= 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \frac{(ix)^6}{6!} + \frac{(ix)^7}{7!} + \frac{(ix)^8}{8!} + \cdots \\[8pt]
&{}= 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - \frac{x^6}{6!} - \frac{ix^7}{7!} + \frac{x^8}{8!} + \cdots \\[8pt]
&{}= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \cdots \right) + i\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right) \\[8pt]
&{}= \cos x + i\sin x \ .
\end{align}](http://upload.wikimedia.org/math/8/7/9/8799ab90dd91d47cf82ea7b449556230.png)
In the last step we have simply recognized the
Taylor series for
sin(x) and
cos(x). The rearrangement of terms is justified because each series is
absolutely convergent.
Using calculus
Treating
i as a constant, albeit an imaginary constant, note that

Then define the function

Because the product rule holds for complex valued functions of a real variable for the same reason as in the real case, the
derivative of ƒ(
x) according to the
product rule is:

Therefore, ƒ(
x) must be a
constant function in
x. Because ƒ(0) = 1 by inspection, ƒ(
x) = 1, giving

Multiplying both sides by cos
x +
i sin
x, we obtain

Using differential equations
Here is another proof that follows from the differential identity above. Define a new function ƒ(
x) of the real variable
x as

Then we may check that

Thus ƒ(
x) and
eix satisfy the same first-order
ordinary differential equation (here the complex values are considered as points in the plane ℝ
2). Note also that both functions are equal to 1 at
x = 0, then by the uniqueness of solutions to ordinary differential equations they must be equal everywhere (see
Picard–Lindelöf theorem and note the comments concerning global uniqueness in the proof section there).
See also
References
- ^ Moskowitz, Martin A. (2002). A Course in Complex Analysis in One Variable. World Scientific Publishing Co.. pp. 7. ISBN 981-02-4780-X.
- ^ Feynman, Richard P. (1977). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. 22–10. ISBN 0-201-02010-6.
- ^ Feynman, Richard P. (1977). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. 22–1. ISBN 0-201-02010-6.
- ^ John Stillwell (2002). Mathematics and Its History. Springer.
External links

The
exponential function ez can be defined as the
limit of
(1 + z/N)N, as
N approaches infinity, and thus
eiπ is the limit of
(1 + iπ/N)N. In this animation
N takes various increasing values from 1 to 100. The computation of
(1 + iπ/N)N is displayed as the combined effect of
N repeated multiplications in the
complex plane, with the final point being the actual value of
(1 + iπ/N)N. It can be seen that as
N gets larger
(1 + iπ/N)N approaches a limit of −1.
In
analytical mathematics,
Euler's Identity, named for the Swiss-German
mathematician Leonhard Euler, is the equality

where
 is Euler's number, the base of natural logarithms,
is Euler's number, the base of natural logarithms,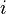 is the imaginary unit, which satisfies i2 = −1, and
is the imaginary unit, which satisfies i2 = −1, and is pi, the ratio of the circumference of a circle to its diameter.
is pi, the ratio of the circumference of a circle to its diameter.
Euler's Identity is also sometimes called
Euler's Equation.
Beauty
Euler's identity is considered by many to be remarkable for its
mathematical beauty. These three basic
arithmetic operations occur exactly once each:
addition,
multiplication, and
exponentiation. The identity also links five fundamental
mathematical constants:
- The number 0, the additive identity.
- The number 1, the multiplicative identity.
- The number π, which is ubiquitous in trigonometry, the geometry of Euclidean space, and analytical mathematics (π = 3.14159265...)
- The number e, the base of natural logarithms, which occurs widely in mathematical and scientific analysis (e = 2.718281828...). Both π and e are transcendental numbers.
- The number i, the imaginary unit of the complex numbers, a field of numbers that contains the roots of all polynomials (that are not constants), and whose study leads to deeper insights into many areas of algebra and calculus, such as integration in calculus.
Furthermore, in
algebra and other areas of mathematics,
equations are commonly written with zero on one side of the
equals sign.
A poll of readers conducted by
The Mathematical Intelligencer magazine named
Euler's Identity as the "most beautiful theorem in mathematics".
[1] Another poll of readers that was conducted by
Physics World magazine, in 2004, chose Euler's Identity tied with
Maxwell equations (of
electromagnetism) as the "greatest equation ever".
[2]
An entire 400-page mathematics book,
Dr. Euler's Fabulous Formula (published in 2006), written by Dr. Paul Nahin (a
Professor Emeritus at the
University of New Hampshire), is devoted to Euler's Identity. This monograph states that Euler's Identity sets "the gold standard for mathematical beauty."
[3]
Constance Reid claimed that Euler's Identity was "the most famous formula in all mathematics."
[4]
The
mathematician Carl Friedrich Gauss was reported to have commented that if this formula was not immediately apparent to a student upon being told it, that student would never become a first-class mathematician.
[5]
After proving Euler's Identity during a lecture,
Benjamin Peirce, a noted American 19th century
philosopher/mathematician and a professor at
Harvard University, stated that "It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth."
[6]
The
Stanford University mathematics professor, Dr.
Keith Devlin, said, "Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's Equation reaches down into the very depths of existence."
[7]
Derivation

Euler's formula for a general angle
The identity is a special case of
Euler's formula from
complex analysis, which states that

for any
real number x. (Note that the arguments to the
trigonometric functions
sine and
cosine are taken to be in
radians, and not in degrees.) In particular,

Since

and

it follows that

which gives the identity
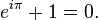
Generalizations
Euler's Identity is actually a special case of the more general identity that the
nth
roots of unity, for
n > 1, add up to 0:

Euler's identity is the case where
n = 2.
In another field of mathematics, by using
quaternion exponentiation, one can show that a similar identity also applies to quaternions:

Attribution
While Euler wrote about his formula that relates
e with
cosine and
sine terms, in the field of complex numbers, there is no known record of Euler's actually stating or deriving the simplified identity equation itself.
Furthermore, Euler's formula was probably known before the life of Euler.
[8] (If so, then this usage would be an example of
Stigler's law of eponymy.) Thus, the question of whether or not this identity should be attributed to Euler is unanswerable.
See also
Notes
- ^ Nahin, 2006, p.2–3 (poll published in the summer 1990 issue of the magazine).
- ^ Crease, 2004.
- ^ Cited in Crease, 2007.
- ^ Reid.
- ^ Derbyshire p.210.
- ^ Maor p.160 and Kasner & Newman p.103–104.
- ^ Nahin, 2006, p.1.
- ^ Sandifer.
References
- Crease, Robert P., "The greatest equations ever", PhysicsWeb, October 2004 (registration required).
- Crease, Robert P. "Equations as icons," PhysicsWeb, March 2007 (registration required).
- Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (New York: Penguin, 2004).
- Kasner, E., and Newman, J., Mathematics and the Imagination (Bell and Sons, 1949).
- Maor, Eli, e: The Story of a number (Princeton University Press, 1998), ISBN 0-691-05854-7
- Nahin, Paul J., Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills (Princeton University Press, 2006), ISBN 978-0691118222
- Reid, Constance, From Zero to Infinity (Mathematical Association of America, various editions).
- Sandifer, Ed, "Euler's Greatest Hits", MAA Online, February 2007.




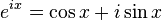







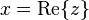 the real part
the real part the imaginary part
the imaginary part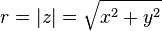 the
the 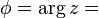
 is the
is the 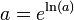






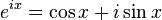
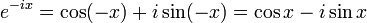
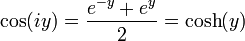

![\begin{align}
\cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\
& = \frac{1}{2}\cdot \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2} \\
& = \frac{1}{2} \left[ \underbrace{ \frac{e^{i(x+y)} + e^{-i(x+y)}}{2} }_{\cos(x+y)} + \underbrace{ \frac{e^{i(x-y)} + e^{-i(x-y)}}{2} }_{\cos(x-y)} \right] \ .
\end{align}](http://upload.wikimedia.org/math/4/5/3/453afc84086fb72dbe8dc2bd17eed023.png)
![\begin{align}
\cos(nx) & = \mathrm{Re} \{\ e^{inx}\ \}
= \mathrm{Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot (e^{ix} + e^{-ix} - e^{-ix})\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot \underbrace{(e^{ix} + e^{-ix})}_{2\cos(x)} - e^{i(n-2)x}\ \} \\
& = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x] \ .
\end{align}](http://upload.wikimedia.org/math/a/7/e/a7e33560e9ae009ce7eb56b99babb19d.png)
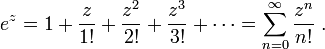


![\begin{align}
e^{ix} &{}= 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \frac{(ix)^6}{6!} + \frac{(ix)^7}{7!} + \frac{(ix)^8}{8!} + \cdots \\[8pt]
&{}= 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - \frac{x^6}{6!} - \frac{ix^7}{7!} + \frac{x^8}{8!} + \cdots \\[8pt]
&{}= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \cdots \right) + i\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right) \\[8pt]
&{}= \cos x + i\sin x \ .
\end{align}](http://upload.wikimedia.org/math/8/7/9/8799ab90dd91d47cf82ea7b449556230.png)










 is
is 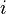 is the
is the  is
is