The Privileged Character of 3+1 Spacetime

There are two kinds of dimensions, spatial (bidirectional) and temporal (unidirectional). Let the number of spatial dimensions be N and the number of temporal dimensions be T. That N = 3 and T = 1, setting aside the compactified dimensions invoked by string theory and undetectable to date, can be explained by appealing to the physical consequences of letting N differ from 3 and T differ from 1. The argument is often of ananthropic character.

Immanuel Kant argued that 3-dimensional space was a consequence of the inverse square law of universal gravitation. While Kant's argument is historically important, John D. Barrow says that it "...gets the punch-line back to front: it is the three-dimensionality of space that explains why we see inverse-square force laws in Nature, not vice-versa." (Barrow 2002: 204). This is because the law of gravitation (or any other inverse-square law) follows from the concept of flux and the proportional relationship of flux density and the strength of field. If N = 3, then 3-dimensional solid objects have surface areas proportional to the square of their size in any selected spatial dimension. In particular, a sphere of radius r has area of 4πr ². More generally, in a space of N dimensions, the strength of the gravitational attraction between two bodies separated by a distance of r would be inversely proportional to r^N−1.

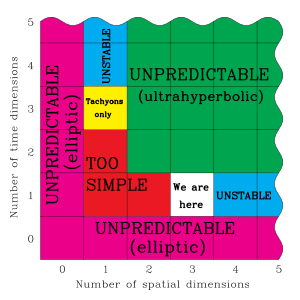
In 1920, Paul Ehrenfest showed that if we fix T = 1 and let N > 3, the orbit of a planet about its sun cannot remain stable. The same is true of a star's orbit around the center of its galaxy.^[13] Ehrenfest also showed that if N is even, then the different parts of a wave impulse will travel at different speeds. If N > 3 and odd, then wave impulses become distorted. Only when N = 3 or 1 are both problems avoided. In 1922, Hermann Weyl showed that Maxwell's theory of electromagnetism works only when N = 3 and T = 1, writing that this fact "...not only leads to a deeper understanding of Maxwell's theory, but also of the fact that the world is four dimensional, which has hitherto always been accepted as merely 'accidental,' become intelligible through it."^[14] Finally, Tangherlini^[15] showed in 1963 that when N > 3, electron orbitals around nuclei cannot be stable; electrons would either fall into the nucleus or disperse.

Properties of n+m-dimensional spacetimes

Max Tegmark^[16] expands on the preceding argument in the following anthropic manner. If T differs from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equations. In such a universe, intelligent life capable of manipulating technology could not emerge. Moreover, if T > 1, Tegmark maintains that protons and electrons would be unstable and could decay into particles having greater mass than themselves. (This is not a problem if the particles have a sufficiently low temperature.) If N > 3, Ehrenfest's argument above holds; atoms as we know them (and probably more complex structures as well) could not exist. If N < 3, gravitation of any kind becomes problematic, and the universe is probably too simple to contain observers. For example, when N < 3, nerves cannot cross without intersecting.

In general, it is not clear how physical law could function if T differed from 1. If T > 1, subatomic particles which decay after a fixed period would not behave predictably, because time-like geodesics would not be necessarily maximal.^[17] N = 1 and T = 3 has the peculiar property that the speed of light in a vacuum is a lower bound on the velocity of matter; all matter consists of tachyons.^[16]

Hence anthropic and other arguments rule out all cases except N = 3 and T = 1—which happens to describe the world about us. Curiously, the cases N = 3 or 4 have the richest and most difficult geometry and topology. There are, for example, geometric statements whose truth or falsity is known for all N except one or both of 3 and 4.^{[citation needed]} N = 3 was the last case of the Poincaré conjecture to be proved.

For an elementary treatment of the privileged status of N = 3 and T = 1, see chpt. 10 (esp. Fig. 10.12) of Barrow;^[18] for deeper treatments, see §4.8 of Barrow and Tipler (1986) and Tegmark.^[16] Barrow has repeatedly cited the work of Whitrow.^[19]

String theory hypothesizes that matter and energy are composed of tiny vibrating strings of various types, most of which are embedded in dimensions that exist only on a scale no larger than the Planck length. Hence N = 3 and T = 1 do not characterize string theory, which embeds vibrating strings in coordinate grids having 10, or even 26, dimensions.

The Causal dynamical triangulation (CDT) theory is a background independent theory which derives the observed 3+1 spacetime from a minimal set of assumptions, and needs no adjusting factors. It does not assume any pre-existing arena (dimensional space), but rather attempts to show how the spacetime fabric itself evolves. It shows spacetime to be 2-d near the Planck scale, and reveals a fractal structure on slices of constant time, but spacetime becomes 3+1-d in scales significantly larger than Planck. So, CDT may become the first theory which doesn't postulate but really explains observed number of spacetime dimensions.<sup>[20]

from Wikipedia's article on "Spacetime." For the full entry click HERE

I discovered this from reading a comment at Peter Woit's "Not Even Wrong" blog, here, which deconstructs the ridiculous Japanese hype that a computer simulation has "proven" Super String Theory.</sup>