
A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), as well as two diverging ultraparallel lines.

Differential geometry is a mathematical discipline that uses the methods of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis for its initial development in the eighteenth and nineteenth century. Since the late nineteenth century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. It is closely related to differential topology, and to the geometric aspects of the theory of differential equations. Grigori Perelman's proof of the Poincaré conjecture using the techniques of Ricci flow demonstrated the power of the differential-geometric approach to questions in topology and highlighted the important role played by the analytic methods. Differential geometry of surfaces already captures many of the key ideas and techniques characteristic of the field.
Contents |
Branches of differential geometry
Riemannian geometry
Riemannian geometry studies Riemannian manifolds, smooth manifolds with a Riemannian metric, a notion of a distance expressed by means of a smooth positive definite symmetric bilinear form defined on the tangent space at each point. Riemannian geometry generalizes Euclidean geometry to spaces that are not necessarily flat, although they still resemble the Euclidean space at each point "infinitesimally", i.e. in the first order of approximation. Various concepts based on length, such as the arc length of curves, area of plane regions, and volume of solids all admit natural analogues in Riemannian geometry. The notion of a directional derivative of a function from multivariable calculus is extended in Riemannian geometry to the notion of a covariant derivative of a tensor. Many concepts and techniques of analysis and differential equations have been generalized to the setting of Riemannian manifolds.
A distance-preserving diffeomorphism between Riemannian manifolds is called an isometry. This notion can also be defined locally, i.e. for small neighborhoods of points. Any two regular curves are locally isometric. However, Theorema Egregium of Gauss showed that already for surfaces, the existence of a local isometry imposes strong compatibility conditions on their metrics: the Gaussian curvatures at the corresponding points must be the same. In higher dimensions, the Riemann curvature tensor is an important pointwise invariant associated to a Riemannian manifold that measures how close it is to being flat. An important class of Riemannian manifolds is formed by the Riemannian symmetric spaces, whose curvature is not necessarily constant. They are the closest to the "ordinary" plane and space considered in Euclidean and non-Euclidean geometry.
Pseudo-Riemannian geometry
Pseudo-Riemannian geometry generalizes Riemannian geometry to the case in which the metric tensor need not be positive-definite. A special case of this is a Lorentzian manifold which is the mathematical basis of Einstein's general relativity theory of gravity.
Finsler geometry
Finsler geometry has the Finsler manifold as the main object of study — this is a differential manifold with a Finsler metric, i.e. a Banach norm defined on each tangent space. A Finsler metric is a much more general structure than a Riemannian metric. A Finsler structure on a manifold M is a function F : TM → [0,∞) such that:
- F(x, my) = |m|F(x,y) for all x, y in TM,
- F is infinitely differentiable in TM − {0},
- The vertical Hessian of F2 is positive definite.
Symplectic geometry
Symplectic geometry is the study of symplectic manifolds. An almost symplectic manifold is a differentiable manifold equipped with a smoothly varying non-degenerate skew-symmetric bilinear form on each tangent space, i.e., a nondegenerate 2-form ω, called the symplectic form. A symplectic manifold is an almost symplectic manifold for which the symplectic form ω is closed: dω = 0.
A diffeomorphism between two symplectic manifolds which preserves the symplectic form is called a symplectomorphism. Non-degenerate skew-symmetric bilinear forms can only exist on even dimensional vector spaces, so symplectic manifolds necessarily have even dimension. In dimension 2, a symplectic manifold is just a surface endowed with an area form and a symplectomorphism is an area-preserving diffeomorphism. The phase space of a mechanical system is a symplectic manifold and they made an implicit appearance already in the work of Lagrange on analytical mechanics and later in Jacobi's and Hamilton's formulation of classical mechanics.
By contrast with Riemannian geometry, where the curvature provides a local invariant of Riemannian manifolds, Darboux's theorem states that all symplectic manifolds are locally isomorphic. The only invariants of a symplectic manifold are global in nature and topological aspects play a prominent role in symplectic geometry. The first result in symplectic topology is probably the Poincaré-Birkhoff theorem, conjectured by Henri Poincaré and proved by George Birkhoff in 1912. It claims that if an area preserving map of an annulus twists each boundary component in opposite directions, then the map has at least two fixed points.[1]
Contact geometry
Contact geometry deals with certain manifolds of odd dimension. It is close to symplectic geometry and like the latter, it originated in questions of classical mechanics. A contact structure on a (2n+1)-dimensional manifold M is given by a smooth hyperplane field H in the tangent bundle that is as far as possible from being associated with the level sets of a differentiable function on M (the technical term is "completely nonintegrable tangent hyperplane distribution"). Near each point p, a hyperplane distribution is determined by a nowhere vanishing 1-form α, which is unique up to multiplication by a nowhere vanishing function:
A local 1-form on M is a contact form if the restriction of its exterior derivative to H is a non-degenerate 2-form and thus induces a symplectic structure on Hp at each point. If the distribution H can be defined by a global 1-form α then this form is contact if and only if the top-dimensional form
is a volume form on M, i.e. does not vanish anywhere. A contact analogue of the Darboux theorem holds: all contact structures on an odd-dimensional manifold are locally isomorphic and can be brought to a certain local normal form by a suitable choice of the coordinate system.
Complex and Kähler geometry
Complex differential geometry is the study of complex manifolds. An almost complex manifold is a real manifold M, endowed with a tensor of type (1,1), i.e. a vector bundle endomorphism (called an almost complex structure)
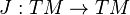 , such that J2 = − 1.
, such that J2 = − 1.
It follows from this definition that an almost complex manifold is even dimensional.
An almost complex manifold is called complex if NJ = 0, where NJ is a tensor of type (2,1) related to J, called the Nijenhuis tensor (or sometimes the torsion). An almost complex manifold is complex if and only if it admits a holomorphic coordinate atlas. An almost Hermitian structure is given by an almost complex structure J, along with a riemannian metric g, satisfying the compatibility condition g(JX,JY) = g(X,Y). An almost hermitian structure defines naturally a differential 2-form ωJ,g(X,Y): = g(JX,Y). The following two conditions are equivalent:
- NJ = 0 and dω = 0,
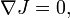
where  is the Levi-Civita connection of g. In this case, (J,g) is called a Kähler structure, and a Kähler manifold is a manifold endowed with a Kähler structure. In particular, a Kähler manifold is both a complex and a symplectic manifold. A large class of Kähler manifolds (the class of Hodge manifolds) is given by all the smooth complex projective varieties.
is the Levi-Civita connection of g. In this case, (J,g) is called a Kähler structure, and a Kähler manifold is a manifold endowed with a Kähler structure. In particular, a Kähler manifold is both a complex and a symplectic manifold. A large class of Kähler manifolds (the class of Hodge manifolds) is given by all the smooth complex projective varieties.
CR geometry
CR geometry is the study of the intrinsic geometry of boundaries of domains in complex manifolds.
Differential topology
Differential topology is the study of (global) geometric invariants without a metric or symplectic form. It starts from the natural operations such as Lie derivative of natual vector bundles and de Rham differential of forms. Beside Lie algebroids, also Courant algebroids start playing a more important role.
Lie groups
A Lie group is a group in the category of smooth manifolds. I.e. beside the algebraic properties this enjoys also differential geometric properties. The most obvious construction is that of a Lie algebra which is the tangent space at the unit endowed with the Lie bracket between left-invariant vector fields. Beside the structure theory there is also the wide field of representation theory.
Bundles and connections
The apparatus of vector bundles, principal bundles, and connections on them plays an extraordinarily important role in the modern differential geometry. A smooth manifold always carries a natural vector bundle, the tangent bundle. Loosely speaking, this structure by itself is sufficient only for developing analysis on the manifold, while doing geometry requires in addition some way to relate the tangent spaces at different points, i.e. a notion of parallel transport. An important example is provided by affine connections. For a surface in R3, tangent planes at different points can be identified using the flat nature of the ambient Euclidean space. In Riemannian geometry, the Levi-Civita connection serves a similar purpose. More generally, differential geometers consider spaces with a vector bundle and a connection as a replacement for the notion of a Riemannian manifold. In this approach, the bundle is external to the manifold and has to be specified as a part of the structure, while the connection provides a further enhancement. In physics, the manifold may be the spacetime and bundles and connections correspond to various physical fields.
Intrinsic versus extrinsic
Initially and up to the middle of the nineteenth century, differential geometry was studied from the extrinsic point of view: curves and surfaces were considered as lying in a Euclidean space of higher dimension (for example a surface in an ambient space of three dimensions). The simplest results are those in the differential geometry of curves and differential geometry of surfaces. Starting with the work of Riemann, the intrinsic point of view was developed, in which one cannot speak of moving 'outside' the geometric object because it is considered as given in a free-standing way. The fundamental result here is Gauss's theorema egregium, to the effect that Gaussian curvature is an intrinsic invariant.
The intrinsic point of view is more flexible. For example, it is useful in relativity where space-time cannot naturally be taken as extrinsic (what would be 'outside' it?). With the intrinsic point of view it is harder to define the central concept of curvature and other structures such as connections, so there is a price to pay.
These two points of view can be reconciled, i.e. the extrinsic geometry can be considered as a structure additional to the intrinsic one. (See the Nash embedding theorem.)
Applications of differential geometry
Below are some examples of how differential geometry is applied to other fields of science and mathematics.
- In physics, three uses will be mentioned:
- Differential geometry is the language in which Einstein's general theory of relativity is expressed. According to the theory, the universe is a smooth manifold equipped with pseudo-Riemannian metric, which described the curvature of space-time. Understanding this curvature is essential for the positioning of satellites into orbit around the earth. Differential geometry is also indispensable in the study of gravitational lensing and black holes.
- Differential forms are useful in the study of electromagnetism.
- Differential geometry has applications to both Lagrangian mechanics and Hamiltonian mechanics. Symplectic manifolds in particular can be used to study Hamiltonian systems.
- In economics, differential geometry has applications to the field of econometrics[2].
- Geometric modeling (including computer graphics) and computer-aided geometric design draw on ideas from differential geometry.
- In engineering, differential geometry can be applied to solve problems in digital signal processing[3].
- In probability, statistics, and information theory, one can interpret various structures as Riemannian manifolds, which yields the field of information geometry, particularly via the Fisher information metric.
- In structural geology, differential geometry is used to analyze and describe geologic structures.
- In computer vision, differential geometry is used to analyze shapes.[4]
See also
- Integral geometry
- List of differential geometry topics
- Glossary of differential geometry and topology
- Important publications in differential geometry
- Important publications in differential topology
- Basic introduction to the mathematics of curved spacetime
- Affine differential geometry
- Projective differential geometry
- Noncommutative geometry
- Synthetic differential geometry
- Abstract differential geometry
- Discrete differential geometry
- Analysis on fractals
Notes
- ^ It is easy to show that the area preserving condition (or the twisting condition) cannot be removed. Note that if one tries to extend such a theorem to higher dimensions, one would probably guess that a volume preserving map of a certain type must have fixed points. This is false in dimensions greater than 3.
- ^ Paul Marriott and Mark Salmon (editors), "Applications of Differential Geometry to Econometrics", Cambridge University Press; 1 edition (September 18, 2000).
- ^ Jonathan H. Manton, "On the role of differential geometry in signal processing" [1].
- ^ Mario Micheli, "The Differential Geometry of Landmark Shape Manifolds: Metrics, Geodesics, and Curvature", http://www.math.ucla.edu/~micheli/PUBLICATIONS/micheli_phd.pdf
References
- Wolfgang Kühnel (2005). Differential Geometry: Curves - Surfaces - Manifolds (2nd ed. ed.). ISBN 0-821-83988-8.
- Theodore Frankel (2004). The geometry of physics: an introduction (2nd ed. ed.). ISBN 0-521-53927-7.
- Spivak, Michael (1999). A Comprehensive Introduction to Differential Geometry (5 Volumes) (3rd Edition ed.).
- do Carmo, Manfredo (1976). Differential Geometry of Curves and Surfaces. ISBN 0-13-212589-7. Classical geometric approach to differential geometry without tensor analysis.
- Kreyszig, Erwin (1991). Differential Geometry. ISBN 0-48-666721-9. Good classical geometric approach to differential geometry with tensor machinery.
- do Carmo, Manfredo Perdigao (1994). Riemannian Geometry.
- McCleary, John (1994). Geometry from a Differentiable Viewpoint.
- Bloch, Ethan D. (1996). A First Course in Geometric Topology and Differential Geometry.
- Gray, Alfred (1998). Modern Differential Geometry of Curves and Surfaces with Mathematica (2nd ed. ed.).
- Burke, William L. (1985). Applied Differential Geometry.
- ter Haar Romeny, Bart M. (2003). Front-End Vision and Multi-Scale Image Analysis. ISBN 1-4020-1507-0.
External links
- B. Conrad. Differential Geometry handouts, Stanford University
- Michael Murray's online differential geometry course, 1996
- A Modern Course on Curves and Surface, Richard S Palais, 2003
- Richard Palais's 3DXM Surfaces Gallery
- Balázs Csikós's Notes on Differential Geometry
- Modern Differential Geometry for Maple
- N. J. Hicks, Notes on Differential Geometry, Van Nostrand.
- MIT OpenCourseWare: Differential Geometry, Fall 2008
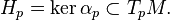
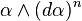













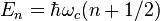 , where ωc = eB/m is the cyclotron frequency. These orbitals are known as
, where ωc = eB/m is the cyclotron frequency. These orbitals are known as 