In
mathematics,
division by zero is a term used if the divisor (denominator) is
zero. Such a division can be formally expressed as
a / 0 where
a is the dividend (numerator). Whether this
expression can be assigned a
well-defined value depends upon the mathematical setting. In ordinary (
real number) arithmetic, the expression has
no meaning, as there is no number which, multiplied by 0, gives
a (
a≠0).
In
computer programming, an attempt to divide by zero may, depending on the programming language and the type of number being divided by zero, generate an exception, generate an error message, crash the program being executed, generate either positive or negative infinity, or could result in a special
not-a-number value (see
below).
Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to
a / 0 is contained in
George Berkeley's criticism of
infinitesimal calculus in
The Analyst; see
Ghosts of departed quantities.
In elementary arithmetic
When division is explained at the
elementary arithmetic level, it is often considered as a description of dividing a
set of objects into equal parts. As an example, consider having ten apples, and these apples are to be distributed equally to five people at a table. Each person would receive

= 2 apples. Similarly, if there are 10 apples, and only one person at the table, that person would receive
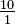
= 10 apples.
So for dividing by zero – what is the number of apples that each person receives when 10 apples are evenly distributed amongst 0 people? Certain words can be pinpointed in the question to highlight the problem. The problem with this question is the "when". There is no way to distribute 10 apples amongst 0 people. In
mathematical jargon, a set of 10 items cannot be
partitioned into 0 subsets. So
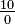
, at least in elementary arithmetic, is said to be meaningless, or undefined.
Similar problems occur if one has 0 apples and 0 people, but this time the problem is in the phrase "
the number". A partition is possible (of a set with 0 elements into 0 parts), but since the partition has 0 parts,
vacuously every set in our partition has a given number of elements, be it 0, 2, 5, or 1000. If there are, say, 5 apples and 2 people, the problem is in "evenly distribute". In any integer partition of a 5-set into 2 parts, one of the parts of the partition will have more elements than the other.
In all of the above three cases,
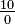
,

and

, one is asked to consider an impossible situation before deciding what the answer will be, and that is why the operations are undefined in these cases.
To understand division by zero, one must check it with multiplication: multiply the quotient by the divisor to get the original number. However, no number multiplied by zero will produce a product other than zero. To satisfy division by zero, the quotient must be bigger than all other numbers, i.e., infinity. This connection of division by zero to infinity takes us beyond elementary arithmetic (see below).
A recurring theme even at this elementary stage is that for every undefined arithmetic operation, there is a corresponding question that is not well-defined. "How many apples will each person receive under a fair distribution of ten apples amongst three people?" is a question that is not well-defined because there can be no fair distribution of ten apples amongst three people.
There is another way, however, to explain the division: if one wants to find out how many people, who are satisfied with half an apple, can one satisfy by dividing up one apple, one divides 1 by 0.5. The answer is 2. Similarly, if one wants to know how many people, who are satisfied with nothing, can one satisfy with 1 apple, one divides 1 by 0. The answer is infinite; one can satisfy infinite people, that are satisfied with nothing, with 1 apple.
Clearly, one cannot extend the operation of division based on the elementary combinatorial considerations that first define division, but must construct new number systems.
Early attempts
The
Brahmasphutasiddhanta of
Brahmagupta (598–668) is the earliest known text to treat
zero as a number in its own right and to define operations involving zero.
[1] The author failed, however, in his attempt to explain division by zero: his definition can be easily proven to lead to algebraic absurdities. According to Brahmagupta,
A positive or negative number when divided by zero is a fraction with the zero as denominator. Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator. Zero divided by zero is zero.
In 830,
Mahavira tried unsuccessfully to correct Brahmagupta's mistake in his book in
Ganita Sara Samgraha: "A number remains unchanged when divided by zero."
[1]
Bhaskara II tried to solve the problem by defining (in modern notation)

.
[1] This definition makes some sense, as discussed below, but can lead to paradoxes if not treated carefully. These paradoxes were not treated until modern times.
In algebra
It is generally regarded among mathematicians that a natural way to interpret division by zero is to first define division in terms of other arithmetic operations. Under the standard rules for arithmetic on
integers,
rational numbers,
real numbers, and
complex numbers, division by zero is undefined. Division by zero must be left undefined in any mathematical system that obeys the axioms of a
field. The reason is that
division is defined to be the inverse operation of
multiplication. This means that the value of
a/
b is the solution
x of the equation
bx =
a whenever such a value exists and is unique. Otherwise the value is left undefined.
For
b = 0, the equation
bx =
a can be rewritten as 0
x =
a or simply 0 =
a. Thus, in this case, the equation
bx =
a has
no solution if
a is not equal to 0, and has
any x as a solution if
a equals 0. In either case, there is no unique value, so
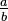
is undefined. Conversely, in a
field, the expression
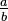
is
always defined if
b is not equal to zero.
Division as the inverse of multiplication
The concept that explains
division in algebra is that it is the inverse of multiplication. For example,

since 2 is the value for which the unknown quantity in

is true. But the expression

requires a value to be found for the unknown quantity in

But any number multiplied by 0 is 0 and so there is no number that solves the equation.
The expression

requires a value to be found for the unknown quantity in

Again, any number multiplied by 0 is 0 and so this time every number solves the equation instead of there being a single number that can be taken as the value of 0/0.
In general, a single value can't be assigned to a fraction where the denominator is 0 so the value remains undefined (see below for other applications).
Fallacies based on division by zero
It is possible to disguise a special case of division by zero in an
algebraic argument,
[1] leading to
spurious proofs that 1 = 2 such as the following:
With the following assumptions:

The following must be true:

Dividing by zero gives:
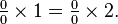
Simplified, yields:

The
fallacy is the implicit assumption that dividing by 0 is a legitimate operation.
In calculus
Extended real line
At first glance it seems possible to define
a/0 by considering the
limit of
a/
b as
b approaches 0.
For any positive
a, the limit from the right is

however, the limit from the left is
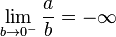
and so the

is undefined (the limit is also undefined for negative
a).
Furthermore, there is no obvious definition of 0/0 that can be derived from considering the limit of a ratio. The limit
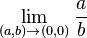
does not exist. Limits of the form

in which both
ƒ(
x) and
g(
x) approach 0 as
x approaches 0, may equal any real or infinite value, or may not exist at all, depending on the particular functions
ƒ and
g (see
l'Hôpital's rule for discussion and examples of limits of ratios). These and other similar facts show that the expression 0/0 cannot be
well-defined as a limit.
Formal operations
A
formal calculation is one carried out using rules of arithmetic, without consideration of whether the result of the calculation is well-defined. Thus, it is sometimes useful to think of
a/0, where
a ≠ 0, as being

. This infinity can be either positive, negative, or unsigned, depending on context. For example, formally:

As with any formal calculation, invalid results may be obtained. A logically rigorous as opposed to formal computation would say only that

(Since the
one-sided limits are different, the two-sided limit does not exist in the standard framework of the real numbers. Also, the fraction 1/0 is left
undefined in the
extended real line, therefore it and

are meaningless
expressions.)
Real projective line
The set

is the
real projective line, which is a
one-point compactification of the real line. Here

means an
unsigned infinity, an infinite quantity that is neither positive nor negative. This quantity satisfies

, which is necessary in this context. In this structure,
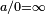
can be defined for nonzero
a, and

. It is the natural way to view the range of the tangent and cotangent functions of
trigonometry: tan(
x) approaches the single point at infinity as
x approaches either

or

from either direction.
This definition leads to many interesting results. However, the resulting algebraic structure is not a
field, and should not be expected to behave like one. For example,

is undefined in the projective line.
Riemann sphere
The set

is the
Riemann sphere, which is of major importance in
complex analysis. Here too

is an unsigned infinity – or, as it is often called in this context, the
point at infinity. This set is analogous to the real projective line, except that it is based on the
field of
complex numbers. In the Riemann sphere,

, but 0/0 is undefined, as is

.
Extended non-negative real number line
The negative real numbers can be discarded, and infinity introduced, leading to the set [0, ∞], where division by zero can be naturally defined as
a/0 = ∞ for positive
a. While this makes division defined in more cases than usual, subtraction is instead left undefined in many cases, because there are no negative numbers.
In higher mathematics
Although division by zero cannot be sensibly defined with real numbers and integers, it is possible to consistently define it, or similar operations, in other mathematical structures.
Non-standard analysis
In the
hyperreal numbers and the
surreal numbers, division by zero is still impossible, but division by non-zero
infinitesimals is possible.
Distribution theory
In
distribution theory one can extend the function

to a distribution on the whole space of real numbers (in effect by using
Cauchy principal values). It does not, however, make sense to ask for a 'value' of this distribution at
x = 0; a sophisticated answer refers to the
singular support of the distribution.
Linear algebra
In
matrix algebra (or
linear algebra in general), one can define a pseudo-division, by setting
a/
b =
ab+, in which
b+ represents the pseudoinverse of
b. It can be proven that if
b−1 exists, then
b+ =
b−1. If
b equals 0, then 0
+ = 0; see
Generalized inverse.
Abstract algebra
Any number system that forms a
commutative ring — for instance, the integers, the real numbers, and the complex numbers — can be extended to a
wheel in which division by zero is always possible; however, in such a case, "division" has a slightly different meaning.
The concepts applied to standard arithmetic are similar to those in more general algebraic structures, such as
rings and
fields. In a field, every nonzero element is invertible under multiplication; as above, division poses problems only when attempting to divide by zero. This is likewise true in a
skew field (which for this reason is called a
division ring). However, in other rings, division by nonzero elements may also pose problems. For example, the ring
Z/6
Z of integers mod 6. The meaning of the expression

should be the solution
x of the equation
2x = 2. But in the ring
Z/6
Z, 2 is not invertible under multiplication. This equation has two distinct solutions,
x = 1 and
x = 4, so the expression

is
undefined.
In field theory, the expression
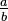
is only shorthand for the formal expression
ab−1, where
b−1 is the multiplicative inverse of
b. Since the field axioms only guarantee the existence of such inverses for nonzero elements, this expression has no meaning when
b is zero. Modern texts include the axiom 0 ≠ 1 to avoid having to consider the
trivial ring or a "
field with one element", where the multiplicative identity coincides with the additive identity.
In computer arithmetic

In the SpeedCrunch calculator application, when a number is divided by zero the answer box displays “Error: Divide by zero”.

Most calculators, such as this Texas Instruments TI-86, will halt execution and display an error message when the user or a running program attempts to divide by zero.
The
IEEE floating-point standard, supported by almost all modern
floating-point units, specifies that every
floating point arithmetic operation, including division by zero, has a well-defined result. The standard supports
signed zero, as well as
infinity and
NaN (
not a number). There are two zeroes, +0 (
positive zero) and −0 (
negative zero) and this removes any ambiguity when dividing. In
IEEE 754 arithmetic,
a ÷ +0 is positive infinity when
a is positive, negative infinity when
a is negative, and NaN when
a = ±0. The infinity signs change when dividing by
−0 instead.
Integer division by zero is usually handled differently from floating point since there is no integer representation for the result. Some processors generate an
exception when an attempt is made to divide an integer by zero, although others will simply continue and generate an incorrect result for the division. The result depends on how division is implemented, and can either be zero, or sometimes the largest possible integer.
Because of the improper algebraic results of assigning any value to division by zero, many computer
programming languages (including those used by
calculators) explicitly forbid the execution of the operation and may prematurely halt a program that attempts it, sometimes reporting a "Divide by zero" error. In these cases, if some special behavior is desired for division by zero, the condition must be explicitly tested (for example, using an
if statement). Some programs (especially those that use
fixed-point arithmetic where no dedicated floating-point hardware is available) will use behavior similar to the IEEE standard, using large positive and negative numbers to approximate infinities. In some programming languages, an attempt to divide by zero results in
undefined behavior.
In
two's complement arithmetic, attempts to divide the smallest signed integer by
− 1 are attended by similar problems, and are handled with the same range of solutions, from explicit error conditions to
undefined behavior.
Most calculators will either return an error or state that 1/0 is undefined, however some
TI and
HP graphing calculators will evaluate (1/0)
2 to ∞.
More advanced
computer algebra systems will return an infinity as a result for division by zero; for instance,
Microsoft Math and
Mathematica will show an
ComplexInfinity result.
Historical accidents
- On September 21, 1997, a divide by zero error on board the USS Yorktown (CG-48) Remote Data Base Manager brought down all the machines on the network, causing the ship's propulsion system to fail.[2]
See also
References
- Patrick Suppes 1957 (1999 Dover edition), Introduction to Logic, Dover Publications, Inc., Mineola, New York. ISBN 0-486-40687-3 (pbk.). This book is in print and readily available. Suppes's §8.5 The Problem of Division by Zero begins this way: "That everything is not for the best in this best of all possible worlds, even in mathematics, is well illustrated by the vexing problem of defining the operation of division in the elementary theory of arithmetic" (p. 163). In his §8.7 Five Approaches to Division by Zero he remarks that "...there is no uniformly satisfactory solution" (p. 166)
- Charles Seife 2000, Zero: The Biography of a Dangerous Idea, Penguin Books, NY, ISBN 0 14 02.9647 6 (pbk.). This award-winning book is very accessible. Along with the fascinating history of (for some) an abhorent notion and others a cultural asset, describes how zero is misapplied with respect to multiplication and division.
- Alfred Tarski 1941 (1995 Dover edition), Introduction to Logic and to the Methodology of Deductive Sciences, Dover Publications, Inc., Mineola, New York. ISBN 0-486-28462-X (pbk.). Tarski's §53 Definitions whose definiendum contains the identity sign discusses how mistakes are made (at least with respect to zero). He ends his chapter "(A discussion of this rather difficult problem [exactly one number satisfying a definiens] will be omitted here.*)" (p. 183). The * points to Exercise #24 (p. 189) wherein he asks for a proof of the following: "In section 53, the definition of the number '0' was stated by way of an example. To be certain this definition does not lead to a contradiction, it should be preceded by the following theorem: There exists exactly one number x such that, for any number y, one has: y + x = y"
Further reading
- Jakub Czajko (July 2004) "On Cantorian spacetime over number systems with division by zero", Chaos, Solitons and Fractals, volume 21, number 2, pages 261–271.
- Ben Goldacre (2006-12-07). "Maths Professor Divides By Zero, Says BBC". http://www.badscience.net/?p=335.
- To Continue with Continuity Metaphysica 6, pp. 91–109, a philosophy paper from 2005, reintroduced the (ancient Indian) idea of an applicable whole number equal to 1/0, in a more modern (Cantorian) style.








 is the
is the  and
and  may appear familiar, their interpretation in the Wheeler–DeWitt equation is substantially different from non-relativistic quantum mechanics.
may appear familiar, their interpretation in the Wheeler–DeWitt equation is substantially different from non-relativistic quantum mechanics.  no longer applies. This property is known as
no longer applies. This property is known as 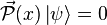
 where
where  plays the role of local time. The role of a Hamiltonian is simply to restrict the space of the "kinematic" states of the Universe to that of "physical" states - the ones that follow gauge orbits. For this reason we call it a "Hamiltonian constraint." Upon quantization, physical states become wave functions that lie in the
plays the role of local time. The role of a Hamiltonian is simply to restrict the space of the "kinematic" states of the Universe to that of "physical" states - the ones that follow gauge orbits. For this reason we call it a "Hamiltonian constraint." Upon quantization, physical states become wave functions that lie in the 










 = 2 apples. Similarly, if there are 10 apples, and only one person at the table, that person would receive
= 2 apples. Similarly, if there are 10 apples, and only one person at the table, that person would receive 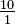 = 10 apples.
= 10 apples.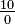 , at least in elementary arithmetic, is said to be meaningless, or undefined.
, at least in elementary arithmetic, is said to be meaningless, or undefined. and
and  , one is asked to consider an impossible situation before deciding what the answer will be, and that is why the operations are undefined in these cases.
, one is asked to consider an impossible situation before deciding what the answer will be, and that is why the operations are undefined in these cases. .
.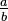 is undefined. Conversely, in a
is undefined. Conversely, in a 







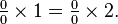


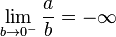
 is undefined (the limit is also undefined for negative a).
is undefined (the limit is also undefined for negative a).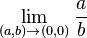

 . This infinity can be either positive, negative, or unsigned, depending on context. For example, formally:
. This infinity can be either positive, negative, or unsigned, depending on context. For example, formally:


 is the
is the  , which is necessary in this context. In this structure,
, which is necessary in this context. In this structure, 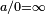 can be defined for nonzero a, and
can be defined for nonzero a, and  . It is the natural way to view the range of the tangent and cotangent functions of
. It is the natural way to view the range of the tangent and cotangent functions of  or
or  from either direction.
from either direction. is undefined in the projective line.
is undefined in the projective line. is the
is the  , but 0/0 is undefined, as is
, but 0/0 is undefined, as is  .
. to a distribution on the whole space of real numbers (in effect by using
to a distribution on the whole space of real numbers (in effect by using  should be the solution x of the equation
should be the solution x of the equation 
