THE man, in this the year 2010, even if he did die in 1906.
| Ludwig Boltzmann | |
|---|---|
 Ludwig Eduard Boltzmann (1844-1906) | |
| Born | February 20, 1844 Vienna, Austrian Empire |
| Died | September 5, 1906 (aged 62) Duino near Trieste, Italy (at that time Austria-Hungary) |
| Residence | Austria, Germany |
| Nationality | Austrian |
| Fields | Physicist |
| Institutions | University of Graz University of Vienna University of Munich University of Leipzig |
| Alma mater | University of Vienna |
| Doctoral advisor | Josef Stefan |
| Doctoral students | Paul Ehrenfest Philipp Frank Gustav Herglotz Franc Hočevar Ignacij Klemenčič Lise Meitner |
| Known for | Boltzmann's constant Boltzmann equation H-theorem Boltzmann distribution Stefan-Boltzmann law |
| Signature | |
Ludwig Eduard Boltzmann (February 20, 1844 – September 5, 1906) was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics. He was one of the most important advocates for atomic theory when that scientific model was still highly controversial.
Contents |
Biography
Childhood and education
Boltzmann was born in Vienna, the capital of the Austrian Empire. His father, Ludwig Georg Boltzmann, was a tax official. His grandfather, who had moved to Vienna from Berlin, was a clock manufacturer, and Boltzmann’s mother, Katharina Pauernfeind, was originally from Salzburg. He received his primary education from a private tutor at the home of his parents. Boltzmann attended high school in Linz, Upper Austria. At age 15, Boltzmann lost his father.
Boltzmann studied physics at the University of Vienna, starting in 1863. Among his teachers were Josef Loschmidt, Joseph Stefan, Andreas von Ettingshausen and Jozef Petzval. Boltzmann received his PhD degree in 1866 working under the supervision of Stefan; his dissertation was on kinetic theory of gases. In 1867 he became a Privatdozent (lecturer). After obtaining his doctorate degree, Boltzmann worked two more years as Stefan’s assistant. It was Stefan who introduced Boltzmann to Maxwell's work.
Academic career
In 1869, at age 25, he was appointed full Professor of Mathematical Physics at the University of Graz in the province of Styria. In 1869 he spent several months in Heidelberg working with Robert Bunsen and Leo Königsberger and then in 1871 he was with Gustav Kirchhoff and Hermann von Helmholtz in Berlin. In 1873 Boltzmann joined the University of Vienna as Professor of Mathematics and there he stayed until 1876.

In 1872, long before women were admitted to Austrian universities, he met Henriette von Aigentler, an aspiring teacher of mathematics and physics in Graz. She was refused permission to unofficially audit lectures, and Boltzmann advised her to appeal; she did, successfully. On July 17, 1876 Ludwig Boltzmann married Henriette von Aigentler; they had three daughters and two sons. Boltzmann went back to Graz to take up the chair of Experimental Physics. Among his students in Graz were Svante Arrhenius and Walther Nernst.[1][2] He spent 14 happy years in Graz and it was there that he developed his statistical concept of nature. In 1885 he became a member of the Imperial Austrian Academy of Sciences and in 1887 he became the President of the University of Graz. He was elected a member of the Royal Swedish Academy of Sciences in 1888.
Boltzmann was appointed to the Chair of Theoretical Physics at the University of Munich in Bavaria, Germany in 1890. In 1893, Boltzmann succeeded his teacher Joseph Stefan as Professor of Theoretical Physics at the University of Vienna.
Final years
Boltzmann spent a great deal of effort in his final years defending his theories. He did not get along with some of his colleagues in Vienna, particularly Ernst Mach, who became a professor of philosophy and history of sciences in 1895. That same year Georg Helm and Wilhelm Ostwald presented their position on Energetics, at a meeting in Lübeck in 1895. They saw energy, and not matter, as the chief component of the universe. However, Boltzmann's position carried the day among other physicists who supported his atomic theories in the debate [3]. Thereafter in 1900, Boltzmann went to the University of Leipzig, on the invitation of Wilhelm Ostwald. After the retirement of Mach due to bad health, Boltzmann came back to Vienna in 1902. His students included Karl Przibram, Paul Ehrenfest and Lise Meitner.
In Vienna, Boltzmann not only taught physics but also lectured on philosophy. Boltzmann’s lectures on natural philosophy were very popular, and received a considerable attention at that time. His first lecture was an enormous success. Even though the largest lecture hall had been chosen for it, the people stood all the way down the staircase. Because of the great successes of Boltzmann’s philosophical lectures, the Emperor invited him for a reception at the Palace.
Boltzmann was subject to rapid alternation of depressed moods with elevated, expansive or irritable moods, likely the symptoms of undiagnosed bipolar disorder. He himself jestingly attributed his rapid swings in temperament to the fact that he was born during the night between Mardi Gras and Ash Wednesday.[4] Meitner relates that those who were close to Boltzmann were aware of his bouts of severe depression and his suicide attempts.
On September 5, 1906, while on a summer vacation in Duino, near Trieste, Boltzmann hanged himself during an attack of depression.[5] He is buried in the Viennese Zentralfriedhof; his tombstone bears the inscription 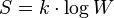 .
.
Philosophy
Boltzmann's kinetic theory of gases seemed to presuppose the reality of atoms and molecules, but almost all German philosophers and many scientists like Ernst Mach and the physical chemist Wilhelm Ostwald opposed their existence. During the 1890s Boltzmann attempted to formulate a compromise position which would allow both atomists and anti-atomists to do physics without arguing over atoms. His solution was to use Hertz's theory that atoms were "Bilder", that is, models or pictures. Atomists could think the pictures were the real atoms while the anti-atomists could think of the pictures as representing a useful but unreal model, but this did not fully satisfy either group. Furthermore, Ostwald and many defenders of "pure thermodynamics" were trying hard to refute the kinetic theory of gases and statistical mechanics because of Boltzmann's assumptions about atoms and molecules and especially statistical interpretation of the second law.
Around the turn of the century, Boltzmann's science was being threatened by another philosophical objection. Some physicists, including Mach's student, Gustav Jaumann, interpreted Hertz to mean that all electromagnetic behavior was continuous as if there were no atoms and molecules and as if all physical behavior was ultimately electromagnetic. This movement around 1900 deeply depressed Boltzmann since it could mean the end of his kinetic theory and statistical interpretation of the second law of thermodynamics.
After Mach's resignation in Vienna in 1901, Boltzmann returned there and decided to become a philosopher himself to refute philosophical objections to his physics, but he soon became discouraged again. In 1904 at a physics conference in St. Louis where most physicists seemed to reject atoms and he was not even invited to the physics section but was stuck in a section called "applied mathematics," he violently attacked philosophy, especially on allegedly Darwinian grounds but actually in terms of Lamarck's theory of the inheritance of acquired characteristics that people inherited bad philosophy from the past and that it was hard for scientists to overcome such inheritance.
In 1905 Boltzmann corresponded extensively with the Austro-German philosopher Franz Brentano in hope of mastering philosophy better apparently so that he could refute its presence in science better, but he became discouraged about this approach as well. In the following year 1906 his mental condition became so bad that he had to resign his position. He committed suicide in September of that same year.
Physics
Boltzmann's most important scientific contributions were in kinetic theory, including the Maxwell-Boltzmann distribution for molecular speeds in a gas. In addition, Maxwell-Boltzmann statistics and the Boltzmann distribution over energies remain the foundations of classical statistical mechanics. They are applicable to the many phenomena that do not require quantum statistics and provide a remarkable insight into the meaning of temperature.
Much of the physics establishment did not share his belief in the reality of atoms and molecules — a belief shared, however, by Maxwell in Scotland and Gibbs in the United States; and by most chemists since the discoveries of John Dalton in 1808. He had a long-running dispute with the editor of the preeminent German physics journal of his day, who refused to let Boltzmann refer to atoms and molecules as anything other than convenient theoretical constructs. Only a couple of years after Boltzmann's death, Perrin's studies of colloidal suspensions (1908-1909) confirmed the values of Avogadro's number and Boltzmann's constant, and convinced the world that the tiny particles really exist.
To quote Planck, "The logarithmic connection between entropy and probability was first stated by L. Boltzmann in his kinetic theory of gases"[6] This famous formula for entropy S is[7] [8]
where k = 1.3806505(24) × 10−23 J K−1 is Boltzmann's constant, and the logarithm is taken to the natural base e. W is the Wahrscheinlichkeit, the frequency of occurrence of a macrostate[9] or, more precisely, the number of possible microstates corresponding to the macroscopic state of a system — number of (unobservable) "ways" in the (observable) thermodynamic state of a system can be realized by assigning different positions and momenta to the various molecules. Boltzmann’s paradigm was an ideal gas of N identical particles, of which Ni are in the i-th microscopic condition (range) of position and momentum. W can be counted using the formula for permutations
where i ranges over all possible molecular conditions. (! denotes factorial.) The "correction" in the denominator is because identical particles in the same condition are indistinguishable.
Boltzmann was also one of the founders of quantum mechanics due to his suggestion in 1877 that the energy levels of a physical system could be discrete.
The equation for S is engraved on Boltzmann's tombstone at the Vienna Zentralfriedhof — his second grave.
The Boltzmann equation

The Boltzmann equation was developed to describe the dynamics of an ideal gas.
where f represents the distribution function of single-particle position and momentum at a given time (see the Maxwell-Boltzmann distribution), F is a force, m is the mass of a particle, t is the time and v is an average velocity of particles.
This equation describes the temporal and spatial variation of the probability distribution for the position and momentum of a density distribution of a cloud of points in single-particle phase space. (See Hamiltonian mechanics.) The first term on the left-hand side represents the explicit time variation of the distribution function, while the second term gives the spatial variation, and the third term describes the effect of any force acting on the particles. The right-hand side of the equation represents the effect of collisions.

In principle, the above equation completely describes the dynamics of an ensemble of gas particles, given appropriate boundary conditions. This first-order differential equation has a deceptively simple appearance, since f can represent an arbitrary single-particle distribution function. Also, the force acting on the particles depends directly on the velocity distribution function f. The Boltzmann equation is notoriously difficult to integrate. David Hilbert spent years trying to solve it without any real success.
The form of the collision term assumed by Boltzmann was approximate. However for an ideal gas the standard Chapman-Enskog solution of the Boltzmann equation is highly accurate. It is expected to lead to incorrect results for an ideal gas only under shock wave conditions.
Boltzmann tried for many years to "prove" the second law of thermodynamics using his gas-dynamical equation — his famous H-theorem. However the key assumption he made in formulating the collision term was "molecular chaos", an assumption which breaks time-reversal symmetry as is necessary for anything which could imply the second law. It was from the probabilistic assumption alone that Boltzmann's apparent success emanated, so his long dispute with Loschmidt and others over Loschmidt's paradox ultimately ended in his failure.
Finally, in the 1970s E.G.D. Cohen and J.R. Dorfman proved that a systematic (power series) extension of the Boltzmann equation to high densities is mathematically impossible. Consequently nonequilibrium statistical mechanics for dense gases and liquids focuses on the Green-Kubo relations, the fluctuation theorem, and other approaches instead.
The Second Law as a law of disorder
The idea that the second law of thermodynamics or "entropy law" is a law of disorder (or that dynamically ordered states are "infinitely improbable") is due to Boltzmann's view of the second law. In particular, his attempt to reduce it to a stochastic collision function, or law of probability following from the random collisions of mechanical particles. Following Maxwell [10], Boltzmann[11] modeled gas molecules as colliding billiard balls in a box, noting that with each collision nonequilibrium velocity distributions (groups of molecules moving at the same speed and in the same direction) would become increasingly disordered leading to a final state of macroscopic uniformity and maximum microscopic disorder or the state of maximum entropy (where the macroscopic uniformity corresponds to the obliteration of all field potentials or gradients). The second law, he argued, was thus simply the result of the fact that in a world of mechanically colliding particles disordered states are the most probable. Because there are so many more possible disordered states than ordered ones, a system will almost always be found either in the state of maximum disorder – the macrostate with the greatest number of accessible microstates such as a gas in a box at equilibrium – or moving towards it. A dynamically ordered state, one with molecules moving "at the same speed and in the same direction," Boltzmann [12] concluded, is thus "the most improbable case conceivable...an infinitely improbable configuration of energy."
Energetics of evolution
Boltzmann's views played an essential role in the development of energetics, the scientific study of energy flows under transformation. In 1922, for example, Alfred J. Lotka referred to Boltzmann as one of the first proponents of the proposition that available energy can be understood as the fundamental object under contention in the biological, or life-struggle and therefore also in the evolution of the organic world.[13] Lotka interpreted Boltzmann's view to imply that available energy could be the central concept that unified physics and biology as a quantitative physical principle of evolution. In the foreword to Boltzmann's Theoretical Physics and Philosophical Problems, S.R. de Groot noted that
| “ | Boltzmann had a tremendous admiration for Darwin and he wished to extend Darwinism from biological to cultural evolution. In fact he considered biological and cultural evolution as one and the same things. ... In short, cultural evolution was a physical process taking place in the brain. Boltzmann included ethics in the ideas which developed in this fashion ... | ” |
Howard T. Odum later sought to develop these views when looking at the evolution of ecological systems, and suggested that the maximum power principle was an example of Darwin's law of natural selection.
See also
- Boltzmann brain
- Boltzmann machine
- History of the molecule
- Lattice Boltzmann methods, a new method in Computational fluid dynamics which utilizes the theories of Boltzmann.
- Philosophy of thermal and statistical physics
- Ludwig Boltzmann Gesellschaft
References
- ^ "Paul Ehrenfest (1880–1933) along with Nernst[,] Arrhenius, and Meitner must be considered among Boltzmann’s most outstanding students."—Jäger, Gustav; Nabl, Josef; Meyer, Stephan (April 1999). "Three Assistants on Boltzmann". Synthese (Springer Netherlands) 119 (1-2): pp. 69–84. doi:10.1023/A:1005239104047. ISSN 1573-0964. http://www.springerlink.com/content/vq5443477m7w7782/. Retrieved 2008-06-09.
- ^ "Walther Hermann Nernst visited lectures by Ludwig Boltzmann"
- ^ New World Encyclopedia contributors, "Ludwig Boltzmann," New World Encyclopedia, (accessed January 31, 2009).[1]
- ^ Ruth Lewin Sime (1996). "Lise Meitner, A Life in Physics". WashingtonPost.com. http://www.washingtonpost.com/wp-srv/style/longterm/books/chap1/lisemeitner.htm. Retrieved 2009-02-06.
- ^ Boltzmann, Ludwig (1995). "Conclusions". in Blackmore, John T.. Ludwig Boltzmann: His Later Life and Philosophy, 1900-1906. 2. Springer. pp. 206–207. ISBN 9780792334644. http://books.google.com/books?id=apip-Jm9WuwC&pg=PA207. Retrieved August 28, 2009.
- ^ Max Planck, p. 119.
- ^ The concept of entropy was introduced by Rudolf Clausius in 1865. He was the first to enunciate the second law of thermodynamics by saying that "entropy always increases".
- ^ An alternative is the information entropy definition introduced in 1948 by Claude Shannon.[2] It was intended for use in communication theory, but is applicable in all areas. It reduces to Boltzmann's expression when all the probabilities are equal, but can, of course, be used when they are not. Its virtue is that it yields immediate results without resorting to factorials or Stirling's approximation. Similar formulas are found, however, as far back as the work of Boltzmann, and explicitly in Gibbs (see reference).
- ^ Pauli, Wolfgang (1973). Statistical Mechanics. Cambridge: MIT Press. ISBN 0-262-66035-0., p. 21
- ^ Maxwell, J. (1871). Theory of heat. London: Longmans, Green & Co.
- ^ Boltzmann, L. (1974). The second law of thermodynamics. Populare Schriften, Essay 3, address to a formal meeting of the Imperial Academy of Science, 29 May, 1886, reprinted in Ludwig Boltzmann, Theoretical physics and philosophical problem, S. G. Brush (Trans.). Boston: Reidel. (Original work published 1886)
- ^ Boltzmann, L. (1974). The second law of thermodynamics. p. 20
- ^ Maximum power principle
Further reading
- Roman Sexl & John Blackmore (eds.), "Ludwig Boltzmann - Ausgewahlte Abhandlungen", (Ludwig Boltzmann Gesamtausgabe, Band 8), Vieweg, Braunschweig, 1982.
- John Blackmore (ed.), "Ludwig Boltzmann - His Later Life and Philosophy, 1900-1906, Book One: A Documentary History", Kluwer, 1995. ISBN 978-0-7923-3231-2
- John Blackmore, "Ludwig Boltzmann - His Later Life and Philosophy, 1900-1906, Book Two: The Philosopher", Kluwer, Dordrecht, Netherlands, 1995. ISBN 978-0-7923-3464-4
- John Blackmore (ed.), "Ludwig Boltzmann - Troubled Genius as Philosopher", in Synthese, Volume 119, Nos. 1 & 2, 1999, pp. 1-232.
- Brush, Stephen G. (ed. & tr.), Boltzmann, Lectures on Gas Theory, Berkeley, CA: U. of California Press, 1964
- Brush, Stephen G. (ed.), Kinetic Theory, New York: Pergamon Press, 1965
- Cercignani, Carlo (1998). Ludwig Boltzmann: The Man Who Trusted Atoms. Oxford: Oxford University Press. ISBN 9780198570646.
- Walter Hoeflechner (ed.), Ludwig Boltzmann - Leben und Briefe, Akademische Druck- u. Verlagsanstalt. Graz, Oesterreich, 1994
- Brush, Stephen G. (1970). "Boltzmann". in Charles Coulston Gillispie (ed.). Dictionary of Scientific Biography. New York: Scribner. ISBN 0-684-16962-2.
- Brush, Stephen G. (1986). The Kind of Motion We Call Heat: A History of the Kinetic Theory of Gases. Amsterdam: North-Holland. ISBN 0-7204-0370-7.
- P. Ehrenfest & T. Ehrenfest (1911) Begriffliche Grundlagen der statistischen Auffassung in der Mechanik, in: Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen. Band IV, 2. Teil ( F. Klein and C. Müller (eds.). Leipzig: Teubner, pp. 3–90. Translated as The conceptual Foundations of the Statistical Approach in Mechanics. New York: Cornell University Press, 1959. ISBN 0-486-49504-3
- Fasol-Boltzmann, Ilse Maria; Gerhard Fasol (1996). Ludwig Boltzmann (1844-1906) Zum hundertsten Todestag. Wien New York: Springer Verlag. ISBN 3-211-33140-9.
- Planck, Max (1914). The Theory of Heat Radiation. P. Blakiston Son & Co. English translation by Morton Masius of the 2nd ed. of Waermestrahlung. Reprinted by Dover (1959) & (1991). ISBN 0-486-66811-8
- Everdell, William R (1988). "The Problem of Continuity and the Origins of Modernism: 1870-1913". History of European Ideas 9 (5): 531–552. doi:10.1016/0191-6599(88)90001-0. ISSN 0191-6599.
- Klein, Martin J. (1973). "The Development of Boltzmann’s Statistical Ideas". in E. G. D. Cohen and W. Thirring (eds). The Boltzmann Equation: Theory and Applications. Acta physica Austriaca Suppl. 10. Wien: Springer. pp. 53–106. ISBN 0-387-81137-0.
- Tolman, Richard C. (1938). The Principles of Statistical Mechanics. Oxford University Press. Reprinted: Dover (1979). ISBN 0-486-63896-0
- Gibbs, J. Willard (1901). Elementary Principles in Statistical Mechanics. Ox Bow Press (1981). ISBN 0-918024-19-6.
- Lindley, David (2001). Boltzmann's Atom: The Great Debate That Launched A Revolution In Physics. New York: Free Press. ISBN 0-684-85186-5.
- Lotka, A. J. (1922). "Contribution to the energetics of evolution" (PDF fulltext). Proc Nat Acad Sci USA 8 (6): 147. doi:10.1073/pnas.8.6.147. ISSN 0027-8424.
- Bronowski, Jacob (1974). "World Within World". The Ascent Of Man. Little Brown & Co. ISBN 978-0-316-10930-7.
- Meyer, Stefan (1904) (in German). Festschrift Ludwig Boltzmann gewidmet zum sechzigsten Geburtstage 20. Februar 1904. J. A. Barth.
External links
- Uffink, Jos (2004). "Boltzmann's Work in Statistical Physics". Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/statphys-Boltzmann/. Retrieved 2007-06-11.
- O'Connor, John J.; Robertson, Edmund F., "Ludwig Boltzmann", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Boltzmann.html.
- "Ludwig Boltzmann," Universität Wien (German).
- Ruth Lewin Sime, Lise Meitner: A Life in Physics Chapter One: Girlhood in Vienna gives Lise Meitner's account of Boltzmann's teaching and career.
- Cohen, E.G.D., 1996, "Boltzmann and Statistical Mechanics."
- Eftekhari, Ali, "Ludwig Boltzmann (1844-1906)." Discusses Boltzmann's philosophical opinions, with numerous quotes.
- Rajasekar, S.; Athavan, N. (2006-09-07). "Ludwig Edward Boltzmann". http://arxiv.org/abs/physics/0609047. Retrieved 2007-05-31.
- Ludwig Boltzmann at the Mathematics Genealogy Project
- Eric W. Weisstein, Boltzmann, Ludwig (1844-1906) at ScienceWorld.
- Ludwig Boltzmann at Find a Grave
- Jacob Bronowski from "The Ascent Of Man"

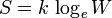
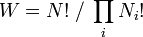
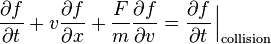
1 comment:
Nice article. Really it is informative and useful. Thanks for sharing this blog.
Post a Comment