 |
| You can buy the ring above for a mere $245 here. One equation to bring them all and in the darkness bind them. In the land of Euler (that would be Switzerland, although Euler did most of his work and lived in St. Petersberg and Prussia). |
Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills by Paul J. Nahin, Professor Emeritus, University of New Hampshire, PhDEE
From + Plus magazine ... Living Mathematics Review by Lewis Dartnell
The hero of this book is Euler's formula:
eiπ + 1 = 0
This simple equation has been widely considered through the last two centuries to be one of the most beautiful formulae of mathematics, and Nahin tells us why.
The constant e is the base of the natural logarithm (and you might have used it in calculations on radioactive decay in physics lessons, for example), whereas &pi, as we all know, is the ratio of a circle's circumference to its diameter. Bothe and &pi are irrational numbers, that is, you could never write down all of their decimal places as they can be proven to continue for ever. The symbol i denotes the square root of -1, a value that does not even exist on the standard number line. Each of these three quantities is therefore curious in its own right, and they were originally developed within very different areas of maths. So how on Earth does ei&pi equal exactly -1? It seems like the biggest fluke in the Universe — and this is part the formula's exquisite beauty. It is also fairly easy to derive the formula yourself, and the proof can be found in any textbook on complex numbers. And as Nahin's book shows, it is also one of the most influential formulae in the history of mathematics.
The book starts off gently enough, with an Introduction leading the reader through a few examples of the most fundamental skill in mathematics; constructing a proof. We see, for example, why √2 must be irrational through a simple proof by contradiction. The process of proving things is mostly ignored at GCSE and A-level, but really does give an eye-opening insight into how real mathematics is often like solving a intriguing puzzle, rather than slogging through homework exercises to practice the basic skills.
Through the following six chapters of the book, Nahin shows us many of the applications of imaginary numbers, Euler's formula, and other mathematical formulae and techniques that have been built on this eighteenth century foundation, both in pure and applied maths. Regular Plusreaders might already know a little bit about some of these, and the sections in the book include: drawing regular prime number polygons, such as the 17-gon, using only a ruler and a compass; how to deconstruct any continuous function, such as a sound wave, into a set of sine waves — a technique that is crucial to modern gadgets like mp3 players. Nahin also shows us the maths of complex numbers lying behind the uncertainty principle of quantum mechanics, listening to the radio, and even how to build a telephone voice scrambler from simple electronics.
The book is well-written and illustrated with numerous diagrams and graphs. For those wanting a little more detail, or to follow up on the bibliography, the book is usefully cross-referenced and has hordes of end notes. But I do have one major warning for Plus readers. Although this book is written to be more easy-reading and popularist than a text book, it is still very heavy-going. More importantly it is pitched at the level of university undergraduates. However, if you're enjoying maths A-level, then this book has a lot to offer, even if you don't understand everything. Every chapter begins with an interesting introduction on the history of a particular problem and the lives of the mathematicians involved, before heading into streams of equations and derivations. The final section of the book gives a detailed biography of the genius behind all of this mathematics through the ages, Leonhard Euler. If you have a class project to write an essay on an influential mathematician, then Euler would certainly be an inspirational choice, and this final chapter a good place to start your research.
We will be discussing two equations. The ring illustrated above is Euler's Identity, which we will discuss second. Feynman's quote refers to Euler's formula, which we will discuss first. From Wikipedia:
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x,
History
It was Bernoulli [1702] who noted thatMeanwhile, Roger Cotes, in 1714, discovered
It was Euler (presumably around 1740) who turned his attention to the exponential function instead of logarithms, and obtained the correct formula now coined after his name. It was published in 1748, and his proof was based on the infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the complex plane arose only some 50 years later (see Caspar Wessel).
Applications in complex number theory
This formula can be interpreted as saying that the function eix traces out the unit circle in the complex number plane as x ranges through the real numbers. Here, x is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in radians.
The original proof is based on the Taylor series expansions of the exponential function ez (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers z.
A point in the complex plane can be represented by a complex number written in cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form reduces the number of terms from two to one, which simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy can be written as
 is the argument of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radians—which is defined up to addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
is the argument of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radians—which is defined up to addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.Now, taking this derived formula, we can use Euler's formula to define the logarithm of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation) that
Therefore, one can write:
Finally, the other exponential law
Relationship to trigonometry
Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:
After the manipulations, the simplified result is still real-valued. For example:
Other applications
In differential equations, the function eix is often used to simplify derivations, even if the final answer is a real function involving sine and cosine. The reason for this is that the complex exponential is the eigenfunction of differentiation. Euler's identity is an easy consequence of Euler's formula.In electrical engineering and other fields, signals that vary periodically over time are often described as a combination of sine and cosine functions (see Fourier analysis), and these are more conveniently expressed as the real part of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.
Definitions of complex exponentiation
Main articles: Exponentiation and Exponential function
The exponential function ex for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of ez for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use either of the two following definitions which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of ex to the complex plane.
Power series definition
For complex zLimit definition
For complex zProofs
Various proofs of the formula are possible.Using power series
Here is a proof of Euler's formula using power series expansions as well as basic facts about the powers of i:Using calculus
Treating i as a constant, albeit an imaginary constant, note thatUsing differential equations
Here is another proof that follows from the differential identity above. Define a new function ƒ(x) of the real variable x asSee also
References
- ^ Moskowitz, Martin A. (2002). A Course in Complex Analysis in One Variable. World Scientific Publishing Co.. pp. 7. ISBN 981-02-4780-X.
- ^ Feynman, Richard P. (1977). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. 22–10. ISBN 0-201-02010-6.
- ^ Feynman, Richard P. (1977). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. 22–1. ISBN 0-201-02010-6.
- ^ John Stillwell (2002). Mathematics and Its History. Springer.
External links
- Proof of Euler's Formula by Julius O. Smith III
- Euler's Formula and Fermat's Last Theorem
- Complex Exponential Function Module by John H. Mathews
- Elements of Algebra
- Visual Representation of Euler's Formula
EULER'S IDENTITY

The exponential function ez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 + iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 + iπ/N)N. It can be seen that as N gets larger (1 + iπ/N)N approaches a limit of −1.
|
In analytical mathematics, Euler's Identity, named for the Swiss-German mathematician Leonhard Euler, is the equality
 is Euler's number, the base of natural logarithms,
is Euler's number, the base of natural logarithms,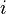 is the imaginary unit, which satisfies i2 = −1, and
is the imaginary unit, which satisfies i2 = −1, and is pi, the ratio of the circumference of a circle to its diameter.
is pi, the ratio of the circumference of a circle to its diameter.
Beauty
Euler's identity is considered by many to be remarkable for its mathematical beauty. These three basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:- The number 0, the additive identity.
- The number 1, the multiplicative identity.
- The number π, which is ubiquitous in trigonometry, the geometry of Euclidean space, and analytical mathematics (π = 3.14159265...)
- The number e, the base of natural logarithms, which occurs widely in mathematical and scientific analysis (e = 2.718281828...). Both π and e are transcendental numbers.
- The number i, the imaginary unit of the complex numbers, a field of numbers that contains the roots of all polynomials (that are not constants), and whose study leads to deeper insights into many areas of algebra and calculus, such as integration in calculus.
A poll of readers conducted by The Mathematical Intelligencer magazine named Euler's Identity as the "most beautiful theorem in mathematics".[1] Another poll of readers that was conducted by Physics World magazine, in 2004, chose Euler's Identity tied with Maxwell equations (of electromagnetism) as the "greatest equation ever".[2]
An entire 400-page mathematics book, Dr. Euler's Fabulous Formula (published in 2006), written by Dr. Paul Nahin (a Professor Emeritus at the University of New Hampshire), is devoted to Euler's Identity. This monograph states that Euler's Identity sets "the gold standard for mathematical beauty."[3]
Constance Reid claimed that Euler's Identity was "the most famous formula in all mathematics."[4]
The mathematician Carl Friedrich Gauss was reported to have commented that if this formula was not immediately apparent to a student upon being told it, that student would never become a first-class mathematician.[5]
After proving Euler's Identity during a lecture, Benjamin Peirce, a noted American 19th century philosopher/mathematician and a professor at Harvard University, stated that "It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth." [6]
The Stanford University mathematics professor, Dr. Keith Devlin, said, "Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's Equation reaches down into the very depths of existence."[7]
Derivation
The identity is a special case of Euler's formula from complex analysis, which states that
Generalizations
Euler's Identity is actually a special case of the more general identity that the nth roots of unity, for n > 1, add up to 0:In another field of mathematics, by using quaternion exponentiation, one can show that a similar identity also applies to quaternions:
Attribution
While Euler wrote about his formula that relates e with cosine and sine terms, in the field of complex numbers, there is no known record of Euler's actually stating or deriving the simplified identity equation itself.Furthermore, Euler's formula was probably known before the life of Euler.[8] (If so, then this usage would be an example of Stigler's law of eponymy.) Thus, the question of whether or not this identity should be attributed to Euler is unanswerable.
See also
Notes
References
- Crease, Robert P., "The greatest equations ever", PhysicsWeb, October 2004 (registration required).
- Crease, Robert P. "Equations as icons," PhysicsWeb, March 2007 (registration required).
- Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (New York: Penguin, 2004).
- Kasner, E., and Newman, J., Mathematics and the Imagination (Bell and Sons, 1949).
- Maor, Eli, e: The Story of a number (Princeton University Press, 1998), ISBN 0-691-05854-7
- Nahin, Paul J., Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills (Princeton University Press, 2006), ISBN 978-0691118222
- Reid, Constance, From Zero to Infinity (Mathematical Association of America, various editions).
- Sandifer, Ed, "Euler's Greatest Hits", MAA Online, February 2007.

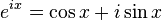







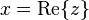 the real part
the real part the imaginary part
the imaginary part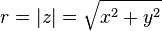 the
the 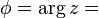
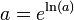






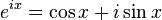
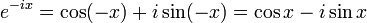
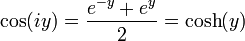

![\begin{align}
\cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\
& = \frac{1}{2}\cdot \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2} \\
& = \frac{1}{2} \left[ \underbrace{ \frac{e^{i(x+y)} + e^{-i(x+y)}}{2} }_{\cos(x+y)} + \underbrace{ \frac{e^{i(x-y)} + e^{-i(x-y)}}{2} }_{\cos(x-y)} \right] \ .
\end{align}](http://upload.wikimedia.org/math/4/5/3/453afc84086fb72dbe8dc2bd17eed023.png)
![\begin{align}
\cos(nx) & = \mathrm{Re} \{\ e^{inx}\ \}
= \mathrm{Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot (e^{ix} + e^{-ix} - e^{-ix})\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot \underbrace{(e^{ix} + e^{-ix})}_{2\cos(x)} - e^{i(n-2)x}\ \} \\
& = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x] \ .
\end{align}](http://upload.wikimedia.org/math/a/7/e/a7e33560e9ae009ce7eb56b99babb19d.png)
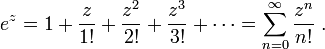


![\begin{align}
e^{ix} &{}= 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \frac{(ix)^6}{6!} + \frac{(ix)^7}{7!} + \frac{(ix)^8}{8!} + \cdots \\[8pt]
&{}= 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - \frac{x^6}{6!} - \frac{ix^7}{7!} + \frac{x^8}{8!} + \cdots \\[8pt]
&{}= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \cdots \right) + i\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right) \\[8pt]
&{}= \cos x + i\sin x \ .
\end{align}](http://upload.wikimedia.org/math/8/7/9/8799ab90dd91d47cf82ea7b449556230.png)















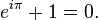


21 comments:
I touch really precise version these articles I stingy there are writers that can create moral stuff.
vector free
I wanted to say that it's nice to know that someone else also mentioned this as I had trouble finding the same info elsewhere. This was the first place that told me the answer www.houseimprovementsuk.com
valuable and excellent design, as share good stuff with good ideas and concepts, lots of great information and inspiration. Thanks for the great information http://www.special-auto-finance.com/
Pscbookmarking.com offers high page rank do follow instant approval blog sites list Instant Approval Blogs
Informative and interesting which we share with you so i think so it is very useful and knowledgeable. I would like to thank you for the efforts. I am tiring the same best work from me in the future as well. what is best technology
That's awesome! I've been cat-and-mouse for that back forever! Thanks a lot for it! stylebeautyfashion.com
This is a very intriguing post, I was looking for this knowledge. Just so you know I located your blog page when I was looking around for blogs like mine, so please check out my site sometime and leave me a comment to let me know what you think. jewelry
After eight a few several weeks of preparing, I just adopted on the water. I adopted some advantage from your page actually. home improvement
I thank you about that. No doubt it will be very useful for my future projects. Would like to see some other posts on the same s technology science
Finally my search has completed! A abundant bare Feature! Thank You SO MUCH! www.fitnashealthcar.com
these pages aren't what they acclimated to be! The source is missing! free gambling casino
Thanks God finally I got that information. I found your article really helpful.
Korean horror movies
Thank you,bless you for the article,I might come back later to view out your other posts. onlineshopper.us
I impress with you post its a interesting and it attract other peoples to read this blog. keep it up.. dating sites
I am sure this paragraph has touched all the internet people, its really really fastidious piece of writing on building up new webpage. website prijs jakency.be
Hope you will not get tired on making posts as informative as this Weslo Cadence G 5.9 Treadmill Review
Most of the time I don’t make comments on websites. background checks
the person who created this post is a genius and knows how to keep the readers connected. Ghana Business News
Post that you talk about this very nice, a lot of new things that I comes from your post. I appreciate your post and look toward more. welcome mat judo
Sometimes injuries can be so cruel as in this case, the injured worker lost her ability to work. There was a huge payout as compensation for the injury provided by the Antigua resort. This is in fact our area of expertise and cases like this are something we see on a weekly basis. To get a payout like Miriam Myers contact the best Personal Injury Claims Scotland which is HD Legal.
Sudden behavioral changes, such as being more reticent or aloof, paying more attention to appearance, and spending more time away from home, are indicators that a spouse may be having an affair. Additionally, they can begin lying, hiding their phone or computer, or altering their spending patterns. These symptoms may point to adultery, although other things can also contribute to them. You can find out if your assumptions are accurate with the aid of a Private Investigators.
Post a Comment