Max Tegmark (born 5 May 1967) is a Swedish-American cosmologist. Tegmark is a professor at the Massachusetts Institute of Technology and belongs to the scientific directorate of the Foundational Questions Institute.
Contents |
[edit]Biography
[edit]Early life
Tegmark was born as Max Shapiro in Sweden, son of Karin Tegmark and Harold S. Shapiro, studied at the Royal Institute of Technology in Stockholm, and later received his Ph.D. from the University of California, Berkeley. After having worked at the University of Pennsylvania, he is now at the Massachusetts Institute of Technology. While still in high-school, Max wrote, and sold commercially, together with school buddy Magnus Bodin a word processor written in pure machine code [1] for the Swedish 8-bit computer ABC80.
[edit]Career
His research has focused on cosmology, combining theoretical work with new measurements to place constraints on cosmological models and their free parameters, often in collaboration with experimentalists. He has over 200 publications, of which 9 have been cited over 500 times.[2] He has developed data analysis tools based on information theory and applied them to Cosmic Microwave Background experiments such as COBE, QMAP, and WMAP, and to galaxy redshift surveys such as the Las Campanas Redshift Survey, the 2dF Survey and the Sloan Digital Sky Survey.
With Daniel Eisenstein and Wayne Hu, he introduced the idea of using Baryon Acoustic Oscillations as a Standard Ruler.[3][non-primary source needed]
With Angelica de Oliveira-Costa and Andrew Hamilton, he discovered the anomalous multipole alignment in the WMAP data sometimes referred to as the "axis of evil".[4][non-primary source needed]
Tegmark has also formulated the "Ultimate ensemble theory of everything", whose only postulate is that "all structures that exist mathematically exist also physically". This simple theory, with no free parameters at all, suggests that in those structures complex enough to contain self-aware substructures (SASs), these SASs will subjectively perceive themselves as existing in a physically "real" world. This idea is formalized as the "Mathematical universe hypothesis" [5]
[edit]Personal life
He was married to astrophysicist Angelica de Oliveira-Costa in 1997, and divorced in 2009. They have two sons, Philip and Alexander.[6]
[edit]In the media
- In 2006, Tegmark was one of fifty scientists interviewed by New Scientist about their predictions for the future. His prediction: "In 50 years, you may be able to buy T-shirts on which are printed equations describing the unified laws of our universes."[7]
- Tegmark appears in the documentary Parallel Worlds, Parallel Lives in which he is interviewed by Mark Oliver Everett, son of the founder of the many-worlds interpretation of quantum mechanics,Hugh Everett.
- Tegmark also appears in "Who's afraid of a big black hole?","What time is it?", "To Infinity and Beyond", "Is Everything We Know About The Universe Wrong?" and "What is Reality?", all part of the BBC's Horizon scientific series of programmes.
[edit]Notes
- ^ [1]
- ^ [2]
- ^ Eisenstein, Daniel J.; Hu, Wayne, Tegmark, Max. "Cosmic Complementarity:
 and
and 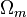 from Combining Cosmic Microwave Background Experiments and Redshift Surveys". The Astrophysical Journal504 (2): L57–L60. arXiv:astro-ph/9805239. Bibcode 1998ApJ...504L..57E. doi:10.1086/311582.
from Combining Cosmic Microwave Background Experiments and Redshift Surveys". The Astrophysical Journal504 (2): L57–L60. arXiv:astro-ph/9805239. Bibcode 1998ApJ...504L..57E. doi:10.1086/311582. - ^ Tegmark, Max; de Oliveira-Costa, Angélica, Hamilton, Andrew (1 December 2003). "High resolution foreground cleaned CMB map from WMAP". Physical Review D 68 (12). arXiv:astro-ph/0302496.Bibcode 2003PhRvD..68l3523T. doi:10.1103/PhysRevD.68.123523.
- ^ Tegmark, Max. "The Mathematical Universe". Foundations of Physics 38 (2): 101–150. Bibcode 2008FoPh...38..101T. doi:10.1007/s10701-007-9186-9. a short version of which is available at Shut up and calculate. (in reference to David Mermin's famous quote "shut up and calculate" [3].
- ^ [4]
- ^ [5]
[edit]External links
| Wikiquote has a collection of quotations related to: Max Tegmark |
In physics and cosmology, the mathematical universe hypothesis (MUH), also known as the Ultimate Ensemble, is a speculative "theory of everything" (TOE) proposed by the theoretical physicist, Max Tegmark.[1]
Contents[hide] |
[edit]Description
Tegmark's mathematical universe hypothesis (MUH) is: Our external physical reality is a mathematical structure. That is, the universe is mathematics in a well-defined sense, and that "in those [worlds] complex enough to contain self-aware substructures [they] will subjectively perceive themselves as existing in a physically 'real' world".[2][3] The hypothesis suggests that worlds corresponding to different sets of initial conditions, physical constants, or altogether different equations may be considered equally real. Tegmark elaborates the MUH into the Computable Universe Hypothesis (CUH), which posits that all computable mathematical structures exist.
The theory can be considered a form of Platonism in that it posits the existence of mathematical entities, can be considered a mathematical monism in that it denies that anything exists except mathematical objects, and can be considered a formal expression of ontic structural realism.
Tegmark claims that the hypothesis has no free parameters and is not observationally ruled out. Thus, he reasons, it is preferred over other theories-of-everything by Occam's Razor. He suggests conscious experience would take the form of mathematical "self-aware substructures" that exist in a physically "'real'" world.
The hypothesis is related to the anthropic principle and to Tegmark's categorization of theories of the multiverse.[4]
Andreas Albrecht of Imperial College in London called it a "provocative" solution to one of the central problems facing physics. Although he "wouldn't dare" go so far as to say he believes it, he noted that "it's actually quite difficult to construct a theory where everything we see is all there is".[5]
[edit]Criticisms and responses
[edit]Definition of the Ensemble
Jürgen Schmidhuber [6] argues that "Although Tegmark suggests that '... all mathematical structures are a priori given equal statistical weight', there is no way of assigning equal nonvanishing probability to all (infinitely many) mathematical structures". Schmidhuber puts forward a more restricted ensemble which admits only universe representations describable by constructive mathematics, that is, computer programs. He explicitly includes universe representations describable by non-halting programs whose output bits converge after finite time, although the convergence time itself may not be predictable by a halting program, due to Kurt Gödel's limitations.[7] In response, Tegmark notes [2] (sec. V.E) that the measure over all universes has not yet been constructed for the String theory landscape either, so this should not be regarded as a "show-stopper".
[edit]Consistency with Gödel's theorem
It has also been suggested that the MUH is inconsistent with Gödel's incompleteness theorem. In a three-way debate between Tegmark and fellow physicists Piet Hut and Mark Alford,[8] the "secularist" (Alford) states that "the methods allowed by formalists cannot prove all the theorems in a sufficiently powerful system... The idea that math is "out there" is incompatible with the idea that it consists of formal systems." Tegmark's response in [8] (sec VI.A.1) is to offer a new hypothesis "that only Godel-complete (fully decidable) mathematical structures have physical existence. This drastically shrinks the Level IV multiverse, essentially placing an upper limit on complexity, and may have the attractive side effect of explaining the relative simplicity of our universe." Tegmark goes on to note that although conventional theories in physics are Godel-undecidable, the actual mathematical structure describing our world could still be Godel-complete, and "could in principle contain observers capable of thinking about Godel-incomplete mathematics, just as finite-state digital computers can prove certain theorems about Godel-incomplete formal systems like Peano arithmetic." In[2] (sec. VII) he gives a more detailed response, proposing as an alternative to MUH the more restricted "Computable Universe Hypothesis" (CUH) which only includes mathematical structures that are simple enough that Gödel's theorem does not require them to contain any undecidable/uncomputable theorems. Tegmark admits that this approach faces "serious challeges", including (a) it excludes much of the mathematical landscape; (b) the measure on the space of allowed theories may itself be uncomputable; and (c) "virtually all historically successful theories of physics violate the CUH".
[edit]Observability
Stoeger, Ellis, and Kircher [9] (sec. 7) note that in a true multiverse theory, "the universes are then completely disjoint and nothing that happens in any one of them is causally linked to what happens in any other one. This lack of any causal connection in such multiverses really places them beyond any scientific support". Ellis [10] (p29) specifically criticizes the MUH, stating that an infinite ensemble of completely disconnected universes is "completely untestable, despite hopeful remarks sometimes made, see, e.g., Tegmark (1998)." Tegmark maintains that MUH is testable, stating that it predicts (a) that "physics research will uncover mathematical regularities in nature", and (b) by assuming that we occupy a typical member of the multiverse of mathematical structures, one could "start testing multiverse predictions by assessing how typical our universe is" (,[2] sec. VIII.C).
[edit]Plausibility of Radical Platonism
The MUH is based on the Radical Platonist view that math is an external reality ([2] sec V.C). However, Jannes [11] argues that "mathematics is at least in part a human construction", on the basis that if it is an external reality then "non-human intelligent beings should exist that understand the language of advanced mathematics. However, none of the non-human intelligent beings that we know of confirm the status of (advanced) mathematics as an objective language." In [8] the secularist argues (sec. VI.A) that math is evolving over time, there is "no reason to think it is converging to a definite structure, with fixed questions and established ways to address them", and also that "The Radical Platonist position is just another metaphysical theory like solipsism... In the end the metaphysics just demands that we use a different language for saying what we already knew." Tegmark responds (sec VI.A.1) that "The notion of a mathematical structure is rigorously defined in any book on Model Theory", and that non-human mathematics would only differ from our own "because we are uncovering a different part of what is in fact a consistent and unified picture, so math is converging in this sense."
[edit]Coexistence of all mathematical structures
Don Page has argued [12] (sec 4) that "At the ultimate level, there can be only one world and, if mathematical structures are broad enough to include all possible worlds or at least our own, there must be one unique mathematical structure that describes ultimate reality. So I think it is logical nonsense to talk of Level 4 in the sense of the co-existence of all mathematical structures." Tegmark responds (,[2] sec. V.E) that "this is less inconsistent with Level IV than it may sound, since many mathematical structures decompose into unrelated substructures, and separate ones can be unified."
[edit]Consistency with our "simple universe"
Alexander Vilenkin comments [13] (Ch.19, p203) that "the number of mathematical structures increases with increasing complexity, suggesting that 'typical' structures should be horrendously large and cumbersome. This seems to be in conflict with the beauty and simplicity of the theories describing our world". He goes on to note (footnote 8, p222) that Tegmark's solution to this problem, the assigning of lower "weights" to the more complex structures ([4] sec. V.B) seems arbitrary ("Who determines the weights?") and may not be logically consistent ("It seems to introduce an additional mathematical structure, but all of them are supposed to be already included in the set").
[edit]See also
- Cosmology
- Digital physics
- Impossible world
- Modal realism
- Multiverse
- Ontology
- String theory
- Theory of everything
- The Unreasonable Effectiveness of Mathematics in the Natural Sciences
[edit]References
- ^ Tegmark, Max (November 1998). "Is "the Theory of Everything" Merely the Ultimate Ensemble Theory?". Annals of Physics 270 (1): 1–51. arXiv:gr-qc/9704009. Bibcode1998AnPhy.270....1T. doi:10.1006/aphy.1998.5855.
- ^ a b c d e f Tegmark, Max (February 2008). "The Mathematical Universe". Foundations of Physics 38 (2): 101–150.arXiv:0704.0646. Bibcode 2008FoPh...38..101T.doi:10.1007/s10701-007-9186-9.
- ^ Tegmark (1998), p. 1.
- ^ a b Tegmark, Max (2003). "Parallel Universes". In Barrow, J.D.; Davies, P.C.W.' & Harper, C.L.. "Science and Ultimate Reality: From Quantum to Cosmos" honoring John Wheeler's 90th birthday. Cambridge University Press. arXiv:astro-ph/0302131.
- ^ Chown, Markus (June 1998). "Anything goes". New Scientist158 (2157 url=http://space.mit.edu/home/tegmark/toe_press.html).
- ^ J. Schmidhuber (2000) "Algorithmic Theories of Everything."
- ^ Schmidhuber, J. (2002). "Hierarchies of generalized Kolmogorov complexities and nonenumerable universal measures computable in the limit". International Journal of Foundations of Computer Science 13 (4): 587–612.doi:10.1142/S0129054102001291.
- ^ a b c Hut, P.; Alford, M.; Tegmark, M. (2006). "On Math, Matter and Mind". Foundations of Physics 36: 765–94.arXiv:physics/0510188. Bibcode 2006FoPh...36..765H.doi:10.1007/s10701-006-9048-x.
- ^ W. R. Stoeger, G. F. R. Ellis, U. Kirchner (2006) "Multiverses and Cosmology: Philosophical Issues."
- ^ G.F.R. Ellis, "83 years of general relativity and cosmology: Progress and problems", Class. Quant. Grav. 16, A37-A75, 1999
- ^ Gil Jannes, "Some comments on 'The Mathematical Universe'", Found. Phys. 39, 397-406, 2009 arXiv:0904.0867
- ^ D. Page, "Predictions and Tests of Multiverse Theories."
- ^ A. Vilenkin (2006) Many Worlds in One: The Search for Other Universes. Hill and Wang, New York.
[edit]Further reading
- Jürgen Schmidhuber (1997) "A Computer Scientist's View of Life, the Universe, and Everything" in C. Freksa, ed., Foundations of Computer Science: Potential - Theory - Cognition. Lecture Notes in Computer Science. Springer: 201-08.
- Tegmark, Max (1998). "Is the 'theory of everything' merely the ultimate ensemble theory?". Annals of Physics 270: 1–51. arXiv:gr-qc/9704009. Bibcode 1998AnPhy.270....1T.doi:10.1006/aphy.1998.5855.
- -------- (2008) "The Mathematical Universe," Foundations of Physics 38: 101-50.
[edit]External links
- Jürgen Schmidhuber "The ensemble of universes describable by constructive mathematics."
- Page maintained by Max Tegmark with links to his technical and popular writings.
- "The 'Everything' mailing list" (and archives). Discusses the idea that all possible universes exist.
- "Is the universe actually made of math?" Interview with Max Tegmark in Discover Magazine.

4 comments:
Hypothesis Testing
Define Hypothesis, what is Hypothesis? Define Hypothesis Testing, null Hypothesis,
http://www.infoaw.com/article.php?articleId=952
thank you for sharing
It is good to read about such professor Jacksonville Tutoring
This is such an informative article St. Petersburg Tutoring
Post a Comment