Ubiquitous in many different fields of science, such recurring constants include π, e and the Feigenbaum constants which are linked to the mathematical models used to describe physical phenomena, Euclidean geometry, analysis and logistic maps respectively. However, mathematical constants such as Apéry's constant and the Golden ratio occur unexpectedly outside of mathematics.
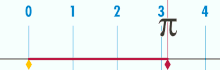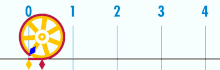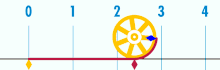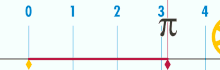
Archimedes' constant π
Pi, though having a natural definition in Euclidean geometry (the circumference of a circle of diameter 1), may be found in many different places in mathematics. Pi is also the circumference of any given circle divided by its diameter.Key examples include the Gaussian integral in complex analysis, nth roots of unity in number theory and Cauchy distributions in probability. However, its universality is not limited to mathematics. Indeed, various formulas in physics, such as Heisenberg's uncertainty principle, and constants such as the cosmological constant bear the constant pi. The presence of pi in physical principles , laws and formulas can have very simple explanations. For example, Coulomb's law, describing the inverse square proportionality of the magnitude of the electrostatic force between two electric charges and their distance, states that, in SI units,
Euler's number e
Euler's Number – also known as the exponential growth constant – e appears in many areas of mathematics, and is defined as the value of the following expression:
Another application of e, discovered in part by Jacob Bernoulli along with French mathematician Pierre Raymond de Montmort, is in the problem of derangements, also known as the hat check problem.[2] Here n guests are invited to a party, and at the door each guest checks his hat with the butler who then places them into labelled boxes. But the butler does not know the name of the guests, and so must put them into boxes selected at random. The problem of de Montmort is: what is the probability that none of the hats gets put into the right box. The answer is
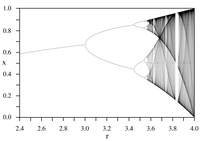
The Feigenbaum constants α and δ
Iterations of continuous maps serve as the simplest examples of models for dynamical systems.[3] Named after mathematical physicist Mitchell Feigenbaum, the two Feigenbaum constants appear in such iterative processes: they are mathematical invariants of logistic maps with quadratic maximum points[4] and their bifurcation diagrams.
The logistic map is a polynomial mapping, often cited as an archetypal example of how chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a seminal 1976 paper by the English biologist Robert May,[5] in part as a discrete-time demographic model analogous to the logistic equation first created by Pierre François Verhulst. The difference equation is intended to capture the two effects of reproduction and starvation.
Apéry's constant ζ(3)

Despite being a special value of the Riemann zeta function, Apéry's constant arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio, computed using quantum electrodynamics.[6] Also, the neuroscientist David Eagleman noted that
where
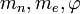 are the neutron mass, the electron mass and the Golden ratio respectively.
are the neutron mass, the electron mass and the Golden ratio respectively.The golden ratio φ
The number
 turns up frequently in geometry, particularly in figures with pentagonal symmetry. Indeed, the length of a regular pentagon's diagonal is
turns up frequently in geometry, particularly in figures with pentagonal symmetry. Indeed, the length of a regular pentagon's diagonal is  times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Also, it appears in the Fibonacci sequence, related to growth by recursion.[8] It is approximately equal to 1.61803398874, or, more precisely
times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Also, it appears in the Fibonacci sequence, related to growth by recursion.[8] It is approximately equal to 1.61803398874, or, more precisely
Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of branches along the stems of plants and of veins in leaves. He extended his research to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, even to the use of proportion in artistic endeavours. In these phenomena he saw the golden ratio operating as a universal law.[9] Zeising wrote in 1854:
[The Golden Ratio is a universal law] in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form.[10]
The Euler–Mascheroni constant γ
The Euler–Mascheroni constant is a recurring constant in number theory. The French mathematician Charles Jean de la Vallée-Poussin proved in 1898 that when taking any positive integer n and dividing it by each positive integer m less than n, the average fraction by which the quotient n/m falls short of the next integer tends to γ as n tends to infinity. Surprisingly, this average doesn't tend to one half. The Euler–Mascheroni constant also appears in Merten's third theorem and has relations to the gamma function, the zeta function and many different integrals and series. The definition of the Euler–Mascheroni constant exhibits a close link between the discrete and the continuous (see curves on the left).



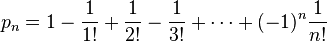





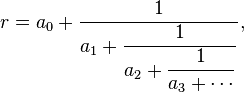
2 comments:
Steven,
I never could find any support for the fact that Montmort really had a solution to the derangement problem. Do you have a reference for that? Just curious (need to correct my notes maybe)..
Nice blog, thanks....
Hm, I had no idea that was controversial. But by following the links in the post, it's either from here:
Grinstead, C.M.; Snell, J.L.. "Introduction to probability theory". p. 85. http://www.dartmouth.edu/~chance/teaching_aids/books_articles/probability_book/book.html. Retrieved 2007-12-09.
or here:
de Montmort, P. R. (1708). Essay d'analyse sur les jeux de hazard. Paris: Jacque Quillau. Seconde Edition, Revue & augmentée de plusieurs Lettres. Paris: Jacque Quillau. 1713.
Although I speak and read no French so i'm not sure about that one.
Then there's John Baez' "Let's Get Deranged." John expositates very clearly on issues of Mathematical Physics.
Post a Comment