I don't know, that's why I'm throwing it out there.
I will present two bits of Fords, the first one lovely and interesting and inspiring from The Math Book, the second the as-exciting-as-watching-paint-dry-or-grass-grow from Wikipedia, which yah, has actual math.
YOU be the judge, and yah, please reply.
I don't bite .... hard. :)
From The Math Book, by Clifford A. Pickover:
Imagine a frothy milkshake with an infinite number of bubbles of all sizes, touching one another but not interpenetrating. The bubbles become smaller and smaller , always filling in the cracks and spaces between larger ones. One form of mysterious froth was discussed by mathematician Lester Ford (1886-1975) in 1938, and it turns out that they characterize the very fabric of our "rational" number system. (Rational numbers are numbers that can be expressed as fractions like 1/2 that can be expressed as fractions).
To create Ford froth, begin by choosing any two integers, h and k. Draw a circle with radius 1/(2k^2) and centered at (h/k, 1/(2k^2)). For example, if you select h = 1 and k = 2, you draw a circle at (0.5, 0.125) and with radius 0.125. Continue to place circles for different values of h and k. As your picture becomes denser, you'll notice that none of your circles intersect , although some will be tangent to one another (that is, just kiss one another). Any circle has an infinitude of circle that kisses it.
Consider a godlike archer positioned above the Ford froth with an approximately large y value. To simulate the shooting of the arrow, draw a vertical line from the location of your archer (for example, at x = a) down to the x-axis . (This line is perpendicular to the x-axis.) If a is a rational number , the line must pierce some Ford circle and hit the horizontal x-axis exactly at the circle's point of tangency. However, when the archer's position is at an irrational number (a non-repeating, endless decimal value like pi=3.1415...), it must leave every circle that it enters and then must enter another circle. Thus, the archer's arrow must pass through an infinity of circles! A deeper mathematical study of Ford circles shows that they provide excellent visualizations of different levels of infinity and of Cantor's Transfinite Numbers.
See also: Cantor's Transfinite Numbers (1874), Menger Sponge (1926), and Fractals (1975).
And from Wikipedia (yawn):
In mathematics, a Ford circle is a circle with centre at (p/q, 1/(2q 2)) and radius 1/(2q 2), wherep/q is an irreducible fraction, i.e. p and q are coprime integers. Each Ford circle is tangent to the horizontal axis y = 0.
Contents[hide] |
[edit]History
Ford circles are a special case of mutually tangent circles; the base line can be thought of as a circle with infinite radius. Systems of mutually tangent circles were studied by Apollonius of Perga, after whom the problem of Apollonius and the Apollonian gasket are named. In the 17th century René Descartes discovered Descartes' theorem, a relationship between the reciprocals of the radii of mutually tangent circles.
Ford circles also appear in the Sangaku (geometrical puzzles) of Japanese mathematics. A typical problem, which is presented on an 1824 tablet in the Gunma Prefecture, covers the relationship of three touching circles with a common tangent. Given the size of the two outer large circles, what is the size of the small circle between then? The answer is equivalent to a Ford circle:
Ford circles are named after American mathematician Lester R. Ford, Sr., who described them in an article in American Mathematical Monthly in 1938, volume 45, number 9, pages 586–601.
[edit]Properties
The Ford circle associated with the fraction p/q is denoted by C[p/q] or C[p, q]. There is a Ford circle associated with every rational number. In addition, the line y = 1 is counted as a Ford circle – it can be thought of as the Ford circle associated with infinity, which is the case p = 1, q = 0.
Two different Ford circles are either disjoint or tangent to one another. No two interiors of Ford circles intersect – even though there is a Ford circle tangent to the x-axis at each point on it with rational co-ordinates. If p/q is between 0 and 1, the Ford circles that are tangent to C[p/q] can be described variously as
- the circles C[r/s] where |ps − qr| = 1,
- the circles associated with the fractions r/s that are the neighbours of p/q in some Farey sequence, or
- the circles C[r/s] where r/s is the next larger or the next smaller ancestor to p/q in the Stern–Brocot tree or where p/q is the next larger or next smaller ancestor to r/s.
Ford circles can also be thought of as curves in the complex plane. The modular group of transformations of the complex plane maps Ford circles to other Ford circles.
By interpreting the upper half of the complex plane as a model of the hyperbolic plane (the Poincaré half-plane model) Ford circles can also be interpreted as a tiling of the hyperbolic plane by horocycles. Any two Ford circles are congruent in hyperbolic geometry. If C[p/q] and C[r/s] are tangent Ford circles, then the half-circle joining (p/q, 0) and (r/s, 0) that is perpendicular to the x-axis is a hyperbolic line that also passes through the point where the two circles are tangent to one another.
Ford circles are a sub-set of the circles in the Apollonian gasket generated by the lines y = 0 and y = 1 and the circle C[0/1].
[edit]Total area of Ford circles
There is a link between the area of Ford circles, Euler's totient function φ and the Riemann zeta function.
As no two Ford circles intersect, it follows immediately that the total area of the Ford circles
is less than 1. In fact the total area of these Ford circles is given by a convergent sum, which can be evaluated.
From the definition, the area is
Simplifying this expression gives
where the last equality reflects the Dirichlet generating function of φ(q) as documented on the page for Euler's totient function. Since ζ(4) = π 4/90, this finally becomes
This sum was discussed on es.ciencia.matematicas.[1]
[edit]See also
[edit]References
- ^ Antonio González, Suma interesante, es.ciencia.matematicas, in Spanish.
[edit]External links
- Art and graphics based on Ford circles
- Ford's Touching Circles at cut-the-knot
- Fractions and Circles
- Lester R. Ford's paper, "Fractions", American Mathematical Monthly, volume 45, number 9, pages 586–601, 1938

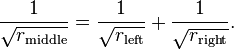
![\left\{ C[p,q]: 0 \le \frac{p}{q} < 1 \right\}](http://upload.wikimedia.org/math/3/c/5/3c59f94359c009b0582ca5a0c8e5cfb2.png)
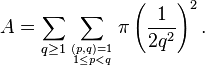
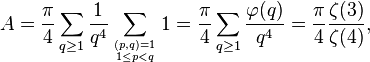

3 comments:
Steven,
Amazing what comes from the simple act of mis-adding fractions. Most of my math mistakes lead to nothing (of value anyway).. Can't resist, the word verification for this is fednest... no kidding.. sounds like what I will have with my government retirement.. a fed nest...
Hey man, I miss you. How ya doin'? When are you parking your retirement keister in Western Kentuck? I have to visit and shake your hand and say howdy to you and Jeannie. You've helped me much. And thanks to Shecky for introducing us.
Well, back on topic. lol. Don't you fret man! You've got a great wife, looks like great kids, you won't want for nothing. As far as government goes, when has it ever been different? As that AWOL soldier in the Texan Confederate Army and my favorite dead American Author once wrote:
"First you have your idiots. Then there's Congressmen. But I repeat yourself."
... Mark Twain
Welcome back to the States, whenever, Pat.
Hi Steve,
The picture you publish in this post reminds me of the exhibition happening at the moment in my Museum. The latter deals with building things out of earth, especially ecological houses. Earth has many pros compared to concrete as concrete is not quite "environment-friendly" ("umweltfreundlich" we say here).
Confused?
Well, to get a hard and solid wall out of earth, the first thing is to guarantee a good compacity of all grains in the wall, which the so-called apollonian arrangement of grains allows and resemble so much that picture you found.
There's also a sort of video game at the exhibition in which you have to place all sorts of round grains in an empty space and find what kind of arrangement make the whole system as solid as possible.
Nice to see that you somehow fell down on this topic, which I deal with everyday now...
Best,
Post a Comment