Every body remains in a state of rest or uniform motion (constant velocity) unless it is acted upon by an external unbalanced force. This means that in the absence of a non-zero net force, the center of mass of a body either remains at rest, or moves at a constant speed in a straight line.
2. Newton's Second Law of Motion
A body of mass m subject to a force F undergoes an acceleration a that has the same direction as the force and a magnitude that is directly proportional to the force and inversely proportional to the mass, i.e., F = ma. Alternatively, the total force applied on a body is equal to the time derivative of linear momentum of the body.
3. Newton's Third Law of Motion
The mutual forces of action and reaction between two bodies are equal, opposite and collinear. This means that whenever a first body exerts a force F on a second body, the second body exerts a force −F on the first body. F and −F are equal in magnitude and opposite in direction. This law is sometimes referred to as the action-reaction law, with F called the "action" and −F the "reaction". The action and the reaction are simultaneous.
4. The First Law of Thermodynamics
Energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed. It is usually formulated by stating that the change in the internal energy of a system is equal to the amount of heat supplied to the system, minus the amount of work performed by the system on its surroundings.
5. The Second Law of Thermodynamics
An expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and explains the phenomenon of irreversibility in nature. The second law declares the impossibility of machines that generate usable energy from the abundant internal energy of nature by processes called perpetual motion of the second kind.
The second law may be expressed in many specific ways, but the first formulation is credited to the German scientist Rudolf Clausius. The law is usually stated in physical terms of impossible processes. In classical thermodynamics, the second law is a basic postulate applicable to any system involving measurable heat transfer, while in statistical thermodynamics, the second law is a consequence of unitarity in quantum theory. In classical thermodynamics, the second law defines the concept of thermodynamic entropy, while in statistical mechanics entropy is defined from information theory, known as the Shannon entropy.
6. The Third Law of Thermodynamics
A statistical law of nature regarding entropy and the impossibility of reaching absolute zero, the null point of the temperature scale. The most common enunciation of the third law of thermodynamics is:
- As a system approaches absolute zero, all processes cease and the entropy of the system approaches a minimum value.
7. The Wheeler-DeWitt Equation
A functional differential equation. It is ill defined in the general case, but very important in theoretical physics, especially in quantum gravity. It is a functional differential equation on the space of three dimensional spatial metrics. The Wheeler–DeWitt equation has the form of an operator acting on a wave functional, the functional reduces to a function in cosmology. Contrary to the general case, the Wheeler–DeWitt equation is well defined in mini-superspaces like the configuration space of cosmological theories. An example of such a wave function is the Hartle–Hawking state.
Bryce DeWitt first published this equation in 1967 under the name “Einstein–Schrodinger equation”; it was later renamed the “Wheeler–DeWitt equation”.[2]
Simply speaking, the Wheeler–DeWitt equation says
 is the Hamiltonian constraint in quantized general relativity. Unlike ordinary quantum field theory or quantum mechanics, the Hamiltonian is a first class constraint on physical states. We also have an independent constraint for each point in space.
is the Hamiltonian constraint in quantized general relativity. Unlike ordinary quantum field theory or quantum mechanics, the Hamiltonian is a first class constraint on physical states. We also have an independent constraint for each point in space.Although the symbols
 and
and  may appear familiar, their interpretation in the Wheeler–DeWitt equation is substantially different from non-relativistic quantum mechanics.
may appear familiar, their interpretation in the Wheeler–DeWitt equation is substantially different from non-relativistic quantum mechanics.  is no longer a spatial wave function in the traditional sense of a complex-valued function that is defined on a 3-dimensional space-like surface and normalized to unity. Instead it is a functional of field configurations on all of spacetime. This wave function contains all of the information about the geometry and matter content of the universe.
is no longer a spatial wave function in the traditional sense of a complex-valued function that is defined on a 3-dimensional space-like surface and normalized to unity. Instead it is a functional of field configurations on all of spacetime. This wave function contains all of the information about the geometry and matter content of the universe.  is still an operator that acts on the Hilbert space of wave functions, but it is not the same Hilbert space as in the nonrelativistic case, and the Hamiltonian no longer determines evolution of the system, so the Schrödinger equation
is still an operator that acts on the Hilbert space of wave functions, but it is not the same Hilbert space as in the nonrelativistic case, and the Hamiltonian no longer determines evolution of the system, so the Schrödinger equation  no longer applies. This property is known as timelessness [disambiguation needed]. The reemergence of time requires the tools of decoherence and clock operators.
no longer applies. This property is known as timelessness [disambiguation needed]. The reemergence of time requires the tools of decoherence and clock operators.We also need to augment the Hamiltonian constraint with momentum constraints
In minisuperspace approximations, we only have one Hamiltonian constraint (instead of infinitely many of them).
In fact, the principle of general covariance in general relativity implies that global evolution per se does not exist; t is just a label we assign to one of the coordinate axes. Thus, what we think about as time evolution of any physical system is just a gauge transformation, similar to that of QED induced by U(1) local gauge transformation
 where
where  plays the role of local time. The role of a Hamiltonian is simply to restrict the space of the "kinematic" states of the Universe to that of "physical" states - the ones that follow gauge orbits. For this reason we call it a "Hamiltonian constraint." Upon quantization, physical states become wave functions that lie in the kernel of the Hamiltonian operator.
plays the role of local time. The role of a Hamiltonian is simply to restrict the space of the "kinematic" states of the Universe to that of "physical" states - the ones that follow gauge orbits. For this reason we call it a "Hamiltonian constraint." Upon quantization, physical states become wave functions that lie in the kernel of the Hamiltonian operator.In general, the Hamiltonian vanishes for a theory with general covariance or time-scaling invariance.


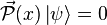
1 comment:
Great Article
IEEE Projects on Information Security
Project Centers in Chennai
JavaScript Training in Chennai
JavaScript Training in Chennai
Post a Comment