Multiplication by Infinity: One, Two, Four, Eight, Who Do We Algebranate?

As you may have noticed, I have changed the name of my blog from the awkward and boring "Current Issues in Mathematical Physics" to "Multiplication by Infinity", a personally cheeky take on "division by zero," the dirty toilet in the Mathematical basement, not to be confused with Dave Richeson's wonderful weblog of the same name.

In Physics and Mathematics, we seek simplicity and bliss via symmetry and conservation laws, which offer many "dualities." But what of "trialities"? Garrett Lisi's continuing exploration into E8 Lie algebra is exploring just that. For this, mayhap, we shall consider Octonions.

What are Octonions, you may ask? Well first, that's an intelligent question. Beats me, I've just started studying them. Fortunately, John Baez wrote an awesome summary in 2001, the introduction of which, below, sums them up quite nicely, complete with Nineteenth Century Mathematical politics.

From Introduction, The Octonions by John Baez, 2001:

There are exactly four normed division algebras: the real numbers   ( $\R$ ), complex numbers ( $\C$ ), quaternions ( $\H$ ), and octonions   ( $\O$ ). The real numbers are the dependable breadwinner of the family,   the complete ordered field we all rely on. The complex numbers are a   slightly flashier but still respectable younger brother: not ordered,   but algebraically complete. The quaternions, being noncommutative, are   the eccentric cousin who is shunned at important family gatherings. But   the octonions are the crazy old uncle nobody lets out of the attic: they   are nonassociative.

Most mathematicians have heard the story of how Hamilton invented the    quaternions. In 1835, at the age of 30, he had discovered how to treat    complex numbers as pairs of real numbers.   Fascinated by the relation    between $\C$ and 2-dimensional geometry, he tried for many years to    invent a bigger algebra that would play a similar role in 3-dimensional    geometry. In modern language, it seems he was looking for a 3-dimensional    normed division algebra. His quest built to its climax in October 1843.    He later wrote to his son, ``Every morning in the early part of the    above-cited month, on my coming down to breakfast, your (then) little    brother William Edwin, and yourself, used to ask me: `Well, Papa, can you    multiply triplets?' Whereto I was always obliged to reply, with a sad    shake of the head: `No, I can only add and subtract them'.''

The problem, of course, was that there exists no 3-dimensional normed     division algebra. He really needed a 4-dimensional algebra.

Finally, on the 16th of October, 1843, while walking with his wife along    the Royal Canal to a meeting of the Royal Irish Academy in Dublin, he made     his momentous discovery. ``That is to say, I then and there felt the     galvanic circuit of thought close; and the sparks which fell from it     were the fundamental equations between $i,j,k$ ; exactly such as I have     used them ever since.'' And in a famous act of mathematical vandalism, he    carved these equations into the stone of the Brougham Bridge:

$\begin{displaymath}i^2 = j^2 = k^2 = ijk = -1 .\end{displaymath}$

One reason this story is so well-known is that Hamilton spent the rest    of his life obsessed with the quaternions and their applications to    geometry [41,49]. And for a while, quaternions were    fashionable. They were made a mandatory examination topic in Dublin,    and in some American universities they were the only advanced    mathematics taught. Much of what we now do with scalars and vectors in    $\R^3$ was then done using real and imaginary quaternions.   A school    of `quaternionists' developed, which was led after Hamilton's death by    Peter Tait of Edinburgh and Benjamin Peirce of Harvard. Tait wrote 8    books on the quaternions, emphasizing their applications to physics.     When Gibbs invented the modern notation for the dot product and cross    product, Tait condemned it as a ``hermaphrodite monstrosity''. A war of    polemics ensued, with luminaries such as Heaviside weighing    in on the side of vectors.

Ultimately the quaternions lost, and    acquired a slight taint of disgrace from which they have never fully    recovered [24].

Less well-known is the discovery of the octonions by Hamilton's friend    from college, John T. Graves. It was Graves' interest in algebra that    got Hamilton thinking about complex numbers and triplets in the first     place. The very day after his fateful walk, Hamilton sent an 8-page    letter describing the quaternions to Graves. Graves replied on October    26th, complimenting Hamilton on the boldness of the idea, but adding    ``There is still something in the system which gravels me. I have not    yet any clear views as to the extent to which we are at liberty    arbitrarily to create imaginaries, and to endow them with supernatural    properties.'' And he asked: ``If with your alchemy you can make three    pounds of gold, why should you stop there?''

Graves then set to work on some gold of his own! On December 26th, he wrote to Hamilton describing a new 8-dimensional algebra, which he called the `octaves'.   He showed that they were a normed division algebra, and used this to express the product of two sums of eight perfect squares as another sum of eight perfect squares: the `eight squares theorem' [48].

In January 1844, Graves sent three letters to Hamilton expanding on his    discovery. He considered the idea of a general theory of    ` $2^m$ -ions', and tried to construct a 16-dimensional normed division    algebra, but he ``met with an unexpected hitch'' and came to doubt that    this was possible. Hamilton offered to publicize Graves' discovery, but    being busy with work on quaternions, he kept putting it off. In July he    wrote to Graves pointing out that the octonions were nonassociative:    `` $A \cdot BC = AB \cdot C = ABC$ , if $A,B,C$ be quaternions, but not    so, generally, with your octaves.'' In fact, Hamilton first invented    the term `associative' at about this time, so the octonions may have    played a role in clarifying the importance of this concept.

Meanwhile the young Arthur Cayley, fresh out of Cambridge, had been thinking about the quaternions ever since Hamilton announced their existence. He seemed to be seeking relationships between the quaternions and hyperelliptic functions. In March of 1845, he published a paper in the Philosophical Magazine entitled `On Jacobi's Elliptic Functions, in Reply to the Rev. B. Bronwin; and on Quaternions' [15]. The bulk of this paper was an attempt to rebut an article pointing out mistakes in Cayley's work on elliptic functions. Apparently as an afterthought, he tacked on a brief description of the octonions. In fact, this paper was so full of errors that it was omitted from his collected works -- except for the part about octonions [16].

Upset at being beaten to publication, Graves attached a postscript to a paper of his own which was to appear in the following issue of the same journal, saying that he had known of the octonions ever since Christmas, 1843. On June 14th, 1847, Hamilton contributed a short note to the Transactions of the Royal Irish Academy, vouching for Graves' priority. But it was too late: the octonions became known as `Cayley numbers'. Still worse, Graves later found that his eight squares theorem had already been discovered by C. F. Degen in 1818 [25,27].

Why have the octonions languished in such obscurity compared to the quaternions? Besides their rather inglorious birth, one reason is that they lacked a tireless defender such as Hamilton. But surely the reason for this is that they lacked any clear application to geometry and physics. The unit quaternions form the group $\SU (2)$ , which is the double cover of the rotation group $\SO (3)$ . This makes them nicely suited to the study of rotations and angular momentum, particularly in the context of quantum mechanics. These days we regard this phenomenon as a special case of the theory of Clifford algebras. Most of us no longer attribute to the quaternions the cosmic significance that Hamilton claimed for them, but they fit nicely into our understanding of the scheme of things.

The octonions, on the other hand, do not. Their relevance to geometry was quite obscure until 1925, when Élie Cartan described `triality' -- the symmetry between vectors and spinors in 8-dimensional Euclidean space [14]. Their potential relevance to physics was noticed in a 1934 paper by Jordan, von Neumann and Wigner on the foundations of quantum mechanics [55]. However, attempts by Jordan and others to apply octonionic quantum mechanics to nuclear and particle physics met with little success. Work along these lines continued quite slowly until the 1980s, when it was realized that the octonions explain some curious features of string theory [60]. The Lagrangian for the classical superstring involves a relationship between vectors and spinors in Minkowski spacetime which holds only in 3, 4, 6, and 10 dimensions. Note that these numbers are 2 more than the dimensions of $\R,\C,\H$ and $\O$ . As we shall see, this is no coincidence: briefly, the isomorphisms

$\begin{displaymath} % latex2html id marker 1518 \begin{array}{lcl} \Sl (2,\R) ... ...&\iso & \so (5,1) \\ \Sl (2,\O) &\iso & \so (9,1) \end{array}\end{displaymath}$

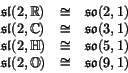
allow us to treat a spinor in one of these dimensions as a pair of elements of the corresponding division algebra. It is fascinating that of these superstring Lagrangians, it is the 10-dimensional octonionic one that gives the most promising candidate for a realistic theory of fundamental physics! However, there is still no proof that the octonions are useful for understanding the real world.

We can only hope that eventually this question will be settled one way or another. Besides their possible role in physics, the octonions are important because they tie together some algebraic structures that otherwise appear as isolated and inexplicable exceptions. As we shall explain, the concept of an octonionic projective space $\OP^n$ only makes sense for $n \le 2$ , due to the nonassociativity of $\O$ . This means that various structures associated to real, complex and quaternionic projective spaces have octonionic analogues only for $n \le 2$ .

Simple Lie algebras are a nice example of this phenomenon. There are 3 infinite families of `classical' simple Lie algebras, which come from the isometry groups of the projective spaces $\RP^n$ , $\CP^n$ and $\HP^n$ . There are also 5 `exceptional' simple Lie algebras. These were discovered by Killing and Cartan in the late 1800s. At the time, the significance of these exceptions was shrouded in mystery: they did not arise as symmetry groups of known structures. Only later did their connection to the octonions become clear. It turns out that 4 of them come from the isometry groups of the projective planes over $\O$ , $\O \tensor \C$ , $\O \tensor \H$ and $\O \tensor \O$ . The remaining one is the automorphism group of the octonions!

Another good example is the classification of simple formally real Jordan algebras. Besides several infinite families of these, there is the `exceptional' Jordan algebra, which consists of $3 \times 3$ hermitian octonionic matrices. Minimal projections in this Jordan algebra correspond to points of $\OP^2$ , and the automorphism group of this algebra is the same as the isometry group of $\OP^2$ .

The octonions also have fascinating connections to topology. In 1957, Raoul Bott computed the homotopy groups of the topological group $\OO (\infty)$ , which is the inductive limit of the orthogonal groups $\OO (n)$ as $n \to \infty$ . He proved that they repeat with period 8:

$\begin{displaymath}\pi_{i+8}(\OO (\infty)) \iso \pi_i(\OO (\infty)). \end{displaymath}$

This is known as `Bott periodicity'. He also computed the first 8:

$\begin{displaymath} % latex2html id marker 1520\begin{array}{lcc} \pi_0(\OO (... ...fty)) &\iso & 0 \\ \pi_7(\OO (\infty)) &\iso & \Z \end{array}\end{displaymath}$

Note that the nonvanishing homotopy groups here occur in dimensions one less than the dimensions of $\R,\C,\H$ , and $\O$ . This is no coincidence! In a normed division algebra, left multiplication by an element of norm one defines an orthogonal transformation of the algebra, and thus an element of $\OO (\infty)$ . This gives us maps from the spheres $S^0, S^1, S^3$ and $S^7$ to $\OO (\infty)$ , and these maps generate the homotopy groups in those dimensions.

Given this, one might naturally guess that the period-8 repetition in the homotopy groups of $\OO (\infty)$ is in some sense `caused' by the octonions. As we shall see, this is true. Conversely, Bott periodicity plays a crucial role in the proof that every division algebra over the reals must be of dimension 1, 2, 4, or 8.

[emphasis Steve's, which hopefully explains this post's title ... that's right, 16 won't work ... you have 4 choices those being 1, 2, 4 or 8]

In what follows we shall try to explain the octonions and their role in algebra, geometry, and topology.

In Section 2 we give four constructions of the octonions: first via their multiplication table, then using the Fano plane, then using the Cayley-Dickson construction and finally using Clifford algebras, spinors, and a generalized concept of `triality' advocated by Frank Adams [1]. Each approach has its own merits.

In Section 3 we discuss the projective lines and planes over the normed division algebras -- especially $\O$ -- and describe their relation to Bott periodicity, the exceptional Jordan algebra, and the Lie algebra isomorphisms listed above.

Finally, in Section 4 we discuss octonionic constructions of the exceptional Lie groups, especially the `magic square'.

Finit for the moment.

And now for some mindless fun:

Multiplication by Infinity

Thursday, December 2, 2010

One, Two, Four, Eight, Who Do We Algebranate?

No comments: