Multiplication by Infinity: Jolt, Snap, Crackle, and Pop

In physics, jerk, also known as jolt (especially in British English), surge and lurch, is the rate of change of acceleration; that is, the derivative of acceleration with respect to time, the second derivative of velocity, or the third derivative of position. Jerk is defined by any of the following equivalent expressions:

$\vec j=\frac {\mathrm{d} \vec a} {\mathrm{d}t}=\frac {\mathrm{d}^2 \vec v} {\mathrm{d}t^2}=\frac {\mathrm{d}^3 \vec s} {\mathrm{d}t^3}$

where

$\vec a$ is acceleration,

$\vec v$ is velocity,

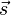$\vec s$ is position

t

is time.

Jerk is a vector, and there is no generally used term to describe its scalar magnitude (e.g. "speed" as the scalar magnitude for velocity).

The units of jerk are metres per second cubed (metres per second per second per second, m/s³ or m·s⁻³). There is no universal agreement on the symbol for jerk, but j is commonly used. ȧ, Newton's notation for the derivative of acceleration, can also be used, especially when "surge" or "lurch" is used instead of "jerk" or "jolt".

Note also the existence of yank—the derivative of force with respect to time, equivalent to the product of mass and jerk.

Applications

Normally force, speed,acceleration is used for analysis of forces. For example, the "jerk" of falling from outerspace to earth is not particularly interesting given the acceleration changes very slowly. Sometimes the analysis has to extend to jerk for a particular reason.

Jerk is often used in engineering, especially when building roller coasters.^{[citation needed]} Some precision or fragile objects—such as passengers, who need time to sense stress changes and adjust their muscle tension or suffer conditions such as whiplash—can be safely subjected not only to a maximum acceleration, but also to a maximum jerk.^{[citation needed]} Jerk may be considered when the excitation of vibrations is a concern. A device that measures jerk is called a "jerkmeter".

Jerk is also important to consider in manufacturing processes. Rapid changes in acceleration of a cutting tool can lead to premature tool wear and result in uneven cuts. This is why modern motion controllers include jerk limitation features.

In mechanical engineering, jerk is considered, in addition to velocity and acceleration, in the development of cam profiles because of tribological implications and the ability of the actuated body to follow the cam profile without chatter.^[1]

Third-order motion profile

In motion control, a common need is to move a system from one steady position to another (point-to-point motion). Following the fastest possible motion within an allowed maximum value for speed, acceleration, and jerk, will result in a third-order motion profile as illustrated below:

The motion profile consists of up to 7 segments defined by the following:^[2]

acceleration build-up, with maximum positive jerk
constant maximum acceleration (zero jerk)
acceleration ramp-down, approaching the desired maximum velocity, with maximum negative jerk
constant maximum speed (zero jerk, zero acceleration)
deceleration build-up, approaching the desired deceleration, with maximum negative jerk
constant maximum deceleration (zero jerk)
deceleration ramp-down, approaching the desired position at zero velocity, with maximum positive jerk

If the initial and final positions are sufficiently close together, the maximum acceleration or maximum velocity may never be reached.

Jerk systems

A jerk system is a system whose behavior is described by a jerk equation, which is an equation of the form (Sprott 2003):

$\frac{\mathrm{d}^3 x}{\mathrm{d} t^3}= f\left(\frac{\mathrm{d}^2 x}{\mathrm{d} t^2},\frac{\mathrm{d} x}{\mathrm{d} t},x\right).$

For example, certain simple electronic circuits may be designed which are described by a jerk equation. These are known as jerk circuits.

One of the most interesting properties of jerk systems is the possibility of chaotic behavior. In fact, certain well-known chaotic systems, such as the Lorenz attractor and the Rössler map, are conventionally described as a system of three first-order differential equations, but which may be combined into a single (although rather complicated) jerk equation.

An example of a jerk equation is:

$\frac{\mathrm{d}^3 x}{\mathrm{d} t^3}+A\frac{\mathrm{d}^2 x}{\mathrm{d} t^2}+\frac{\mathrm{d} x}{\mathrm{d} t}-|x|+1=0.$

Where A is an adjustable parameter. This equation has a chaotic solution for A=3/5 and can be implemented with the following jerk circuit:

In the above circuit, all resistors are of equal value, except

R A = R / A = 5 R / 3

, and all capacitors are of equal size. The dominant frequency will be

1 / 2π R C

. The output of op amp 0 will correspond to the x variable, the output of 1 will correspond to the first derivative of x and the output of 2 will correspond to the second derivative.

Notes

^ Blair, G., "Making the Cam", Race Engine Technology 10, September/October 2005
^ There is an idealization here that the jerk can be changed from zero to a constant non-zero value instantaneously. However, since in classical mechanics all forces are caused by smooth fields, all derivatives of the position are continuous. On the other hand, this is also an idealization; in quantum field theory particles do change momentum discontinuously.

References

Sprott JC (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5.
Sprott JC (1997). "Some simple chaotic jerk functions" (PDF). Am J Phys 65 (6): 537–43. doi:10.1119/1.18585. http://sprott.physics.wisc.edu/pubs/paper229.pdf. Retrieved 2009-09-28.
Blair G (2005). "Making the Cam" (PDF). Race Engine Technology (010). http://www.profblairandassociates.com/pdfs/Camshaft%20RET%20010.pdf. Retrieved 2009-09-29.

External links

What is the term used for the third derivative of position?, description of jerk in the Usenet Physics FAQ.
Mathematics of Motion Control Profiles

THE 4TH AND HIGHER DERIVATIVES

In physics, jounce or snap is the fourth derivative of the position vector with respect to time, with the first, second, and third derivatives being velocity, acceleration, and jerk, respectively; in other words, the jounce is the rate of change of the jerk with respect to time.

$\vec s =\frac {d \vec j} {dt}=\frac {d^2 \vec a} {dt^2}=\frac {d^3 \vec v} {dt^3}=\frac {d^4 \vec r} {dt^4}$

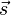The notation $\vec s$ (used in ^[1]) is not to be confused with the displacement vector commonly denoted similarly. Currently, there are no well-accepted designations for the derivatives of jounce.

The fifth and sixth derivatives of position as a function of time are "sometimes somewhat facetiously" ^[1]^[2] referred to (in association with "Snap") as "Crackle" and "Pop" (named after the characters that appear in advertising for Kellogg's Rice Krispies cereal); however, these terms have not gained widespread acceptance.

The SI unit of jounce is metres per second to the power of 4 (metres per second per second per second per second, m/s⁴ or m·s⁻⁴).