Szilassi Polyhedron
Császár
In geometry, the Császár polyhedron (Hungarian pronunciation: [ˈtʃaːsaːr]) is a nonconvex polyhedron, topologically a torus, with 14 triangular faces.
This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph K7 onto the surface of a torus.
The tetrahedron and the Császár polyhedron are the only two known polyhedra (having a manifold boundary) without any diagonals, although there are other known polyhedra such as the Schönhardt polyhedron for which there are no interior diagonals (that is, all diagonals are outside the polyhedron) as well as non-manifold surfaces with no diagonals (Szabó 1984, 2009). If a polyhedron with v vertices is embedded onto a surface with h holes, in such a way that every pair of vertices is connected by an edge, it follows by some manipulation of the Euler characteristic that
The Császár polyhedron is named after Hungarian topologist Ákos Császár, who discovered it in 1949. The dual to the Császár polyhedron, the Szilassi polyhedron, was discovered later, in 1977, by Lajos Szilassi; it has 14 vertices, 21 edges, and seven hexagonal faces, each sharing an edge with every other face. Like the Császár polyhedron, the Szilassi polyhedron has the topology of a torus.
References
- Császár, A. (1949), "A polyhedron without diagonals", Acta Sci. Math. Szeged 13: 140–142.
- Gardner, Martin (1988), Time Travel and Other Mathematical Bewilderments, W. H. Freeman and Company, pp. 139–152, ISBN 0-7167-1924-X
- Gardner, Martin (1992), Fractal Music, Hypercards and More: Mathematical Recreations from Scientific American, W. H. Freeman and Company, pp. 118–120, ISBN 0-7167-2188-0
- Lutz, Frank H. (2001), "Császár's Torus", Electronic Geometry Models: 2001.02.069, http://www.eg-models.de/models/Classical_Models/2001.02.069/.
- Szabó, Sándor (1984), "Polyhedra without diagonals", Periodica Mathematica Hungarica 15 (1): 41–49, doi:10.1007/BF02109370.
- Szabó, Sándor (2009), "Polyhedra without diagonals II", Periodica Mathematica Hungarica 58 (2): 181–187, doi:10.1007/s10998-009-10181-x.
- Ziegler, Günter M. (2008), "Polyhedral surfaces of high genus", in Bobenko, A. I.; Schröder, P.; Sullivan, J. M. et al., Discrete Differential Geometry, Oberwolfach Seminars, 38, Springer-Verlag, pp. 191–213, doi:10.1007/978-3-7643-8621-4_10, math.MG/0412093.
External links
SZILASSI
The Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.
Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem. It has an axis of 180-degree symmetry; three pairs of faces are congruent leaving one unpaired hexagon that has the same rotational symmetry as the polyhedron. The 14 vertices and 21 edges of the Szilassi polyhedron form an embedding of the Heawood graph onto the surface of a torus.
The tetrahedron and the Szilassi polyhedron are the only two known polyhedra in which each face shares an edge with each other face.
If a polyhedron with f faces is embedded onto a surface with h holes, in such a way that each face shares an edge with each other face, it follows by some manipulation of the Euler characteristic that
The Szilassi polyhedron is named after Hungarian mathematician Lajos Szilassi, who discovered it in 1977. The dual to the Szilassi polyhedron, the Császár polyhedron, was discovered earlier by Ákos Császár (1949); it has seven vertices, 21 edges connecting every pair of vertices, and 14 triangular faces. Like the Szilassi polyhedron, the Császár polyhedron has the topology of a torus.
References
- Császár, Ákos (1949), "A polyhedron without diagonals", Acta Sci. Math. Szeged 13: 140–142.
- Gardner, Martin (1978), In Which a Mathematical Aesthetic is Applied to Modern Minimal Art, "Mathematical Games", Scientific American 239: 22–32, doi:10.1038/scientificamerican1178-22.
- Jungerman, M.; Ringel, Gerhard (1980), "Minimal triangulations on orientable surfaces", Acta Mathematica 145 (1–2): 121–154, doi:10.1007/BF02414187.
- Peterson, Ivars (2007), "A polyhedron with a hole", MathTrek, Mathematical Association of America, http://www.maa.org/mathland/mathtrek_01_22_07.html.
- Szilassi, Lajos (1986), "Regular toroids", Structural Topology 13: 69–80, http://haydn.upc.es/people/ros/StructuralTopology/ST13/st13-06-a3-ocr.pdf.
External links
- Ace, Tom, The Szilassi polyhedron, http://www.minortriad.com/szilassi.html.
- Weisstein, Eric W., "Szilassi Polyhedron" from MathWorld.
 |
| Szilassi Polyhedron net |
 |
| Szilassi Polyhedron |
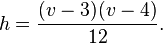

No comments:
Post a Comment