George Boole (1815 - 1864)

The original Working Class Boy Made Good, Boole was born in the wrong time, in the wrong place, and definitely in the wrong class - he didn't have a hope of growing up to be a mathematical genius, but he did it anyway.

Born in the English industrial town of Lincoln, Boole was lucky enough to have a father who passed along his own love of math. Young George took to learning like a politician to a pay rise and, by the age of eight, had outgrown his father's self-taught limits.

A family friend stepped in to teach the boy basic Latin, and was exhausted within a few years. Boole was translating Latin poetry by the age of twelve. By the time he hit puberty, the adolescent George was fluent in German, Italian and French. At 16 he became an assistant teacher, at 20 he opened his own school.

Over the next few years, depending mainly on mathematical journals borrowed from the local Mechanic's Institute, Boole struggled with Isaac Newton's 'Principia' and the works of 18th and 19th century French mathematicians Pierre-Simon Laplace and Joseph-Louis Lagrange. He had soon mastered the most intricate mathematical principles of his day.

It was time to move on. 

At the age of 24, George Boole published his first paper ('Researches on the Theory of Analytical Transformations') in the Cambridge Mathematical Journal. Over the next ten years, his star rose as a steady stream of original articles began to push the limits of mathematics.

By 1844 he was concentrating on the uses of combined algebra and calculus to process infinitely small and large figures, and, in that same year, received a Royal Society medal for his contributions to analysis.

Boole soon began to see the possibilities for applying his algebra to the solution of logical problems. Boole's 1847 work, 'The Mathematical Analysis of Logic', not only expanded on Gottfried Leibniz' earlier speculations on the correlation between logic and math, but argued that logic was principally a discipline of mathematics, rather than philosophy.

It was this paper that won him, not only the admiration of the distinguished logician Augustus de Morgan (a mentor of Ada Byron's), but a place on the faculty of Ireland's Queen's College.



. . . . . . . . . . . . . . . . . . . . Without a school to run, Boole began to delve deeper into his own work, concentrating on refining his 'Mathematical Analysis', and determined to find a way to encode logical arguments into an indicative language that could be manipulated and solved mathematically.

He came up with a type of linguistic algebra, the three most basic operations of which were (and still are) AND, OR and NOT. It was these three functions that formed the basis of his premise, and were the only operations necessary to perform comparisons or basic mathematical functions.

Boole's system (detailed in his 'An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities', 1854) was based on a binary approach, processing only two objects - the yes-no, true-false, on-off, zero-one approach.

Surprisingly, given his standing in the academic community, Boole's idea was either criticised or completely ignored by the majority of his peers. Luckily, American logician Charles Sanders Peirce was more open-minded.

Twelve years after Boole's 'Investigation' was published, Pierce gave a brief speech describing Boole's idea to the American Academy of Arts and Sciences - and then spent more than 20 years modifying and expanding it, realising the potential for use in electronic circuitry and eventually designing a fundamental electrical logic circuit.

Pierce never actually built his theoretical logic circuit, being himself more of a logician than an electrician, but he did introduce boolean algebra into his university logic philosophy courses.

Eventually, one bright student - Claude Shannon - picked up the idea and ran with it.



. . . . . . . . . . . . . . . . . . . . Boole published a number of papers following his 'Investigation', the two most influential probably being a 'Treatise on Differential Equations' (1859) and 'Treatise on the Calculus of Finite Differences' (1860).
Unfortunately, Boole's life was cut short when he died of a 'feverish cold' at the age of 49, after walking 2 miles through the rain to get to class and then lecturing in wet clothes (proving, once again, that genius and common sense sometimes have a less than nodding acquaintance).



. . . . . . . . . . . . . . . . . . . . With George Boole's 'Mathematical Analysis' and 'Investigation', boolean algebra, sometimes known as boolean logic, came into being.

His two value system, separating arguments into different classes which can then be processed according to the presence or absence of a certain property, enabled any proposition - regardless of the number of individual items - to draw logical conclusions.

Boole's texts led to the development of applications he could never have imagined.

Related:
What's So Logical About Boolean Algebra?
Claude Shannon

What's So Logical About Boolean Algebra?


George Boole believed in what he called the ‘process of analysis’, that is, the process by which combinations of interpretable symbols are obtained. It is the use of these symbols according to well-determined methods of combination that he believed presented ‘true calculus’.

Today, all our computers use Boole's logic system - using microchips that contain thousands of tiny electronic switches arranged into logical ‘gates’ that produce predictable and reliable conclusions.

The basic logic gates are AND, OR and NOT. It is these gates, used in different combinations, that allow the computer to execute its operations using binary language.

Each gate assesses information (consisting of high or low voltages) in accordance with predetermined rules, and produces a single high or low voltage logical conclusion. The voltage itself represents the binary yes-no, true-false, one-zero concept.



. . . . . . . . . . . . . . . . . . . .

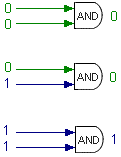AND gates will only yield a TRUE result (that is, a binary 1) if all input is TRUE. Therefore, the top two gates will produce a FALSE (binary 0) result.

OR gates are less fussy. An OR gate will send a TRUE result if any of its input is TRUE. Only if every input is FALSE will it produce a 0 result.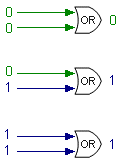

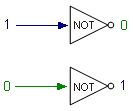NOT gates, on the other hand, do just one thing. A NOT gate accepts only a single input, either TRUE or FALSE, which it promptly reverses. NOT gates can be combined with AND or OR to give NAND (not and) or NOR (not or) gates. These new gates process input in the usual manner and then reverse the result.

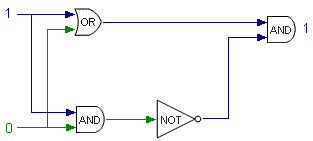
Putting them all together produces something like this (‘this’, by the way, is known as a half-adder). The top gate inputs 1 and 0 through OR to give a 1 result. The bottom gate channels 1 and 0 through AND to produce 0, which is inverted through the NOT gate into a second 1. The last AND gate sees two inputs of 1 and promptly spits out a TRUE (1) result. Thus, 1 + 0 = 1.



. . . . . . . . . . . . . . . . . . . . By adjusting the gates, binary adders can be used not only for addition, but for subtraction, multiplication, and division as well, enabling them to control the computer's data flow and to process instructions.


From KerryR.net"This is an Australian site, and written in Australian English. Any resemblance to American or Euro English is purely coincidental" :-)

© Copyright 1996 Kerry Redshaw Brisbane, Queensland, Australia KerryR.net ABN 94 704 041 474