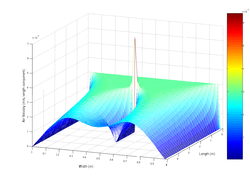
Multiplication by Infinity: Differential equations

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders. Differential equations play a prominent role in engineering, physics, economics, and other disciplines.

Visualization of airflow into a duct modelled using the Navier-Stokes equations, a set of partial differential equations

Differential equations arise in many areas of science and technology: whenever a deterministic relationship involving some continuously varying quantities (modeled by functions) and their rates of change in space and/or time (expressed as derivatives) is known or postulated. This is illustrated in classical mechanics, where the motion of a body is described by its position and velocity as the time varies. Newton's Laws allow one to relate the position, velocity, acceleration and various forces acting on the body and state this relation as a differential equation for the unknown position of the body as a function of time. In some cases, this differential equation (called an equation of motion) may be solved explicitly.
An example of modelling a real world problem using differential equations is determination of the velocity of a ball falling through the air, considering only gravity and air resistance. The ball's acceleration towards the ground is the acceleration due to gravity minus the deceleration due to air resistance. Gravity is constant but air resistance may be modelled as proportional to the ball's velocity. This means the ball's acceleration, which is the derivative of its velocity, depends on the velocity. Finding the velocity as a function of time involves solving a differential equation.
Differential equations are mathematically studied from several different perspectives, mostly concerned with their solutions—the set of functions that satisfy the equation. Only the simplest differential equations admit solutions given by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form. If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have been developed to determine solutions with a given degree of accuracy.

[hide]

Directions of study

The study of differential equations is a wide field in pure and applied mathematics, physics, meteorology, and engineering. All of these disciplines are concerned with the properties of differential equations of various types. Pure mathematics focuses on the existence and uniqueness of solutions, while applied mathematics emphasizes the rigorous justification of the methods for approximating solutions. Differential equations play an important role in modelling virtually every physical, technical, or biological process, from celestial motion, to bridge design, to interactions between neurons. Differential equations such as those used to solve real-life problems may not necessarily be directly solvable, i.e. do not have closed form solutions. Instead, solutions can be approximated using numerical methods.
Mathematicians also study weak solutions (relying on weak derivatives), which are types of solutions that do not have to be differentiable everywhere. This extension is often necessary for solutions to exist, and it also results in more physically reasonable properties of solutions, such as possible presence of shocks for equations of hyperbolic type.
The study of the stability of solutions of differential equations is known as stability theory.

Nomenclature

The theory of differential equations is quite developed and the methods used to study them vary significantly with the type of the equation.

An ordinary differential equation (ODE) is a differential equation in which the unknown function (also known as the dependent variable) is a function of a single independent variable. In the simplest form, the unknown function is a real or complex valued function, but more generally, it may be vector-valued or matrix-valued: this corresponds to considering a system of ordinary differential equations for a single function. Ordinary differential equations are further classified according to the order of the highest derivative with respect to the dependent variable appearing in the equation. The most important cases for applications are first order and second order differential equations. In the classical literature also distinction is made between differential equations explicitly solved with respect to the highest derivative and differential equations in an implicit form.

A partial differential equation (PDE) is a differential equation in which the unknown function is a function of multiple independent variables and the equation involves its partial derivatives. The order is defined similarly to the case of ordinary differential equations, but further classification into elliptic, hyperbolic, and parabolic equations, especially for second order linear equations, is of utmost importance. Some partial differential equations do not fall into any of these categories over the whole domain of the independent variables and they are said to be of mixed type.

Both ordinary and partial differential equations are broadly classified as linear and nonlinear. A differential equation is linear if the unknown function and its derivatives appear to the power 1 (products are not allowed) and nonlinear otherwise. The characteristic property of linear equations is that their solutions form an affine subspace of an appropriate function space, which results in much more developed theory of linear differential equations. Homogeneous linear differential equations are a further subclass for which the space of solutions is a linear subspace i.e. the sum of any set of solutions or multiples of solutions is also a solution. The coefficients of the unknown function and its derivatives in a linear differential equation are allowed to be (known) functions of the independent variable or variables; if these coefficients are constants then one speaks of a constant coefficient linear differential equation.
There are very few methods of explicitly solving nonlinear differential equations; those that are known typically depend on the equation having particular symmetries. Nonlinear differential equations can exhibit very complicated behavior over extended time intervals, characteristic of chaos. Even the fundamental questions of existence, uniqueness, and extendability of solutions for nonlinear differential equations, and well-posedness of initial and boundary value problems for nonlinear PDEs are hard problems and their resolution in special cases is considered to be a significant advance in the mathematical theory (cf Navier–Stokes existence and smoothness).
Linear differential equations frequently appear as approximations to nonlinear equations. These approximations are only valid under restricted conditions. For example, the harmonic oscillator equation is an approximation to the nonlinear pendulum equation that is valid for small amplitude oscillations (see below).

Examples

In the first group of examples, let u be an unknown function of x, and c and ω are known constants.

Inhomogeneous first order linear constant coefficient ordinary differential equation:

$\frac{du}{dx} = cu+x^2.$

Homogeneous second order linear ordinary differential equation:

$\frac{d^2u}{dx^2} - x\frac{du}{dx} + u = 0.$

Homogeneous second order constant coefficient linear ordinary differential equation describing the harmonic oscillator:

$\frac{d^2u}{dx^2} + \omega^2u = 0.$

First order nonlinear ordinary differential equation:

$\frac{du}{dx} = u^2 + 1.$

Second order nonlinear ordinary differential equation describing the motion of a pendulum of length L:

$g\frac{d^2u}{dx^2} + L\sin u = 0.$

In the next group of examples, the unknown function u depends on two variables x and t or x and y.

Homogeneous first order linear partial differential equation:

$\frac{\partial u}{\partial t} + t\frac{\partial u}{\partial x} = 0.$

Homogeneous second order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:

$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0.$

Third order nonlinear partial differential equation, the Korteweg–de Vries equation:

$\frac{\partial u}{\partial t} = 6u\frac{\partial u}{\partial x} - \frac{\partial^3 u}{\partial x^3}.$

Related concepts

A delay differential equation (DDE) is an equation for a function of a single variable, usually called time, in which the derivative of the function at a certain time is given in terms of the values of the function at earlier times.

A stochastic differential equation (SDE) is an equation in which the unknown quantity is a stochastic process and the equation involves some known stochastic processes, for example, the Wiener process in the case of diffusion equations.

A differential algebraic equation (DAE) is a differential equation comprising differential and algebraic terms, given in implicit form.

Connection to difference equations

Universality of mathematical description

Many fundamental laws of physics and chemistry can be formulated as differential equations. In biology and economics differential equations are used to model the behavior of complex systems. The mathematical theory of differential equations first developed, together with the sciences, where the equations had originated and where the results found application. However, diverse problems, sometimes originating in quite distinct scientific fields, may give rise to identical differential equations. Whenever this happens, mathematical theory behind the equations can be viewed as a unifying principle behind diverse phenomena. As an example, consider propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of them may be described by the same second order partial differential equation, the wave equation, which allows us to think of light and sound as forms of waves, much like familiar waves in the water. Conduction of heat, whose theory was developed by Joseph Fourier, is governed by another second order partial differential equation, the heat equation. It turned out that many diffusion processes, while seemingly different, are described by the same equation; Black-Scholes equation in finance is for instance, related to the heat equation.

Notable differential equations

Newton's Second Law in dynamics (mechanics)
Hamilton's equations in classical mechanics
Radioactive decay in nuclear physics
Newton's law of cooling in thermodynamics
The wave equation
Maxwell's equations in electromagnetism
The heat equation in thermodynamics
Laplace's equation, which defines harmonic functions
Poisson's equation
Einstein's field equation in general relativity
The Schrödinger equation in quantum mechanics
The geodesic equation
The Navier–Stokes equations in fluid dynamics
The Lotka–Volterra equation in population dynamics
The Black–Scholes equation in finance
The Cauchy–Riemann equations in complex analysis
The Poisson–Boltzmann equation in molecular dynamics
The shallow water equations
Universal differential equation

Biology

Verhulst equation – biological population growth
von Bertalanffy model – biological individual growth
Lotka–Volterra equations – biological population dynamics
Replicator dynamics – may be found in theoretical biology
Economics

References

This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations. Please improve this article by introducing more precise citations where appropriate. (August 2009)

D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.
A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2.
W. Johnson, A Treatise on Ordinary and Partial Differential Equations, John Wiley and Sons, 1913, in University of Michigan Historical Math Collection
E.L. Ince, Ordinary Differential Equations, Dover Publications, 1956
E.A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, 1955
P. Blanchard, R.L. Devaney, G.R. Hall, Differential Equations, Thompson, 2006

External links

Lectures on Differential Equations MIT Open CourseWare Video
Online Notes / Differential Equations Paul Dawkins, Lamar University
Differential Equations, S.O.S. Mathematics
Introduction to modeling via differential equations Introduction to modeling by means of differential equations, with critical remarks.
Differential Equation Solver Java applet tool used to solve differential equations.
Mathematical Assistant on Web Symbolic ODE tool, using Maxima
Exact Solutions of Ordinary Differential Equations
A bibliography of books about differential equations, from the Mathematical Association of America
Collection of ODE and DAE models of physical systems MATLAB models
Notes on Diffy Qs: Differential Equations for Engineers An introductory textbook on differential equations by Jiri Lebl of UIUC

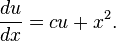
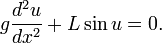
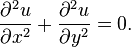
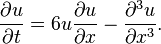
1 comment:

Jérôme Chauvet said...: Differential equations is one of the things I am currently working on. In biochemistry, many logical properties of biological circuitries are in fact emerging properties of underlying dynamical systems which are completely modelled by Ordinary Differential Equations, or Stochastic Differential Equations when including noise. The transition from ODEs systems to logical systems is the hard point biomathematicians have to deal with at present.

As you may know it, I have begun to add non-commutativity to it, but it's not easy at all:)

Best,; February 21, 2010 at 11:27 AM

Multiplication by Infinity

Friday, February 19, 2010

Differential equations

Contents