Thermodynamic Energy <===> Black Hole Mass
Thermodynamic Temperature <===> Black hole surface Gravity
Thermodynamic Entropy <===> Black hole Area
(from page 266 of "From Eternity to Here" by Professor Sean Carroll (no relation to Lewis Carroll)
from Wikipedia:
In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons. Much as the study of the statistical mechanics of black body radiation led to the advent of the theory of quantum mechanics, the effort to understand the statistical mechanics of black holes has had a deep impact upon the understanding of quantum gravity, leading to the formulation of the holographic principle.

An artist depiction of two black holes merging, a process in which the laws of thermodynamics are upheld.
Contents |
Black hole entropy
Black hole entropy is the entropy carried by a black hole.If black holes carried no entropy, it would be possible to violate the second law of thermodynamics by throwing mass into the black hole. The only way to satisfy the second law is to admit that the black holes have entropy whose increase more than compensates for the decrease of the entropy carried by the object that was swallowed.
Starting from theorems proved by Stephen Hawking, Jacob Bekenstein conjectured that the black hole entropy was proportional to the area of its event horizon divided by the Planck area. Later, Hawking showed that black holes emit thermal Hawking radiation corresponding to a certain temperature (Hawking temperature). Using the thermodynamic relationship between energy, temperature and entropy, Hawking was able to confirm Bekenstein's conjecture and fix the constant of proportionality at 1/4:
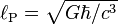 is the Planck length. The black hole entropy is proportional to its area A. The fact that the black hole entropy is also the maximal entropy that can be squeezed within a fixed volume was the main observation that led to the holographic principle. The subscript BH either stands for "black hole" or "Bekenstein-Hawking".
is the Planck length. The black hole entropy is proportional to its area A. The fact that the black hole entropy is also the maximal entropy that can be squeezed within a fixed volume was the main observation that led to the holographic principle. The subscript BH either stands for "black hole" or "Bekenstein-Hawking".Although Hawking's calculations gave further thermodynamic evidence for black hole entropy, until 1995 no one was able to make a controlled calculation of black hole entropy based on statistical mechanics, which associates entropy with a large number of microstates. In fact, so called "no hair" theorems appeared to suggest that black holes could have only a single microstate. The situation changed in 1995 when Andrew Strominger and Cumrun Vafa calculated the right Bekenstein-Hawking entropy of a supersymmetric black hole in string theory, using methods based on D-branes. Their calculation was followed by many similar computations of entropy of large classes of other extremal and near-extremal black holes, and the result always agreed with the Bekenstein-Hawking formula.
Loop quantum gravity, viewed as the main competitor of string theory, also offered a slightly more heuristic calculation of the black hole entropy. This calculation confirms that the entropy is proportional to the surface area, with the proportionality constant dependent on the only free parameter in LQG, Immirzi parameter.
The laws of black hole mechanics
The four laws of black hole mechanics are physical properties that black holes are believed to satisfy. The laws, analogous to the laws of thermodynamics, were discovered by Brandon Carter, Stephen Hawking and James Bardeen.Statement of the laws
The laws of black hole mechanics are expressed in geometrized units.The Zeroth Law
The horizon has constant surface gravity for a stationary black hole.The First Law
We haveThe Second Law
The horizon area is, assuming the weak energy condition, a non-decreasing function of time,The Third Law
It is not possible to form a black hole with vanishing surface gravity. κ = 0 is not possible to achieve.Discussion of the laws
The Zeroth Law
The zeroth law is analogous to the zeroth law of thermodynamics which states that the temperature is constant throughout a body in thermal equilibrium. It suggests that the surface gravity is analogous to temperature. T constant for thermal equilibrium for a normal system is analogous to κ constant over the horizon of a stationary black hole.The First Law
The left hand side, dM, is the change in mass/energy. Although the first term does not have an immediately obvious physical interpretation, the second and third terms on the right hand side represent changes in energy due to rotation and electromagnetism. Analogously, the first law of thermodynamics is a statement of energy conservation, which contains on its right hand side the term T dS.
The Second Law
The second law is the statement of Hawking's area theorem. Analogously, the second law of thermodynamics states that the entropy of an isolated system is a non-decreasing function of time, suggesting a link between entropy and the area of a black hole horizon. However, this version violates the second law of thermodynamics by matter losing (its) entropy as it falls in, giving a decrease in entropy. Generalised second law introduced as total entropy = black hole entropy + outside entropyThe Third Law
Extremal black holes have vanishing surface gravity. Stating that κ cannot go to zero is analogous to the third law of thermodynamics which, in its weak formulation, states that it is impossible to reach absolute zero temperature in a physical process. The strong version of the third law of thermodynamics, which states that as the temperature approaches zero, the entropy also approaches zero, does not have an analogue for black holes. However, the strong version is violated by many known systems in condensed matter physics, and has therefore been rejected as a law.Interpretation of the laws
The four laws of black hole mechanics suggest that one should identify the surface gravity of a black hole with temperature and the area of the event horizon with entropy, at least up to some multiplicative constants. If one only considers black holes classically, then they have zero temperature and, by the no hair theorem, zero entropy, and the laws of black hole mechanics remain an analogy. However, when quantum mechanical effects are taken into account, one finds that black holes emit thermal radiation (Hawking radiation) at temperature .
.
 .
.
Beyond black holes
Hawking and Page showed that black hole thermodynamics is more general than black holes, that cosmological event horizons also have an entropy and temperature.More fundamentally, 't Hooft and Susskind used the laws of black hole thermodynamics to argue for a general Holographic Principle of nature, which asserts that consistent theories of gravity and quantum mechanics must be lower dimensional. Though not yet fully understood in general, the holographic principle is central to theories like the AdS/CFT correspondence.
See also
References
- Bardeen, J. M.; Carter, B.; Hawking, S. W. (1973). "The four laws of black hole mechanics". Communications in Mathematical Physics 31 (2): 161–170. doi:.
- Bekenstein, Jacob D. (April 1973). "Black holes and entropy". Physical Review D 7 (8): 2333–2346. doi:.
- Hawking, Stephen W. (1974). "Black hole explosions?". Nature 248 (5443): 30–31. doi:.
- Hawking, Stephen W. (1975). "Particle creation by black holes". Communications in Mathematical Physics 43 (3): 199–220. doi:.
- Hawking, S. W.; Ellis, G. F. R. (1973). The Large Scale Structure of Space-time. New York: Cambridge University Press. ISBN 0521099064.
- Hawking, Stephen W. (1994). "The Nature of Space and Time". ArΧiv e-print. arΧiv:hep-th/9409195v1.
- 't Hooft, Gerardus (1985). "On the quantum structure of a black hole". Nuclear Phys. B 256: 727–745. doi:. http://igitur-archive.library.uu.nl/phys/2005-0622-153848/14549.pdf.

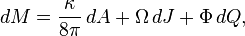
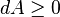
1 comment:
Post a Comment