Thermodynamics

 Wikipedia's entry on this important topic as of Feb. 16, 2020:

In physics, thermodynamics (from the Greek θέρμη therme, meaning "heat"^[1] and δύναμις, dynamis, meaning "power") is the study of energy conversion between heat and mechanical work, and subsequently the macroscopic variables such as temperature, volume and pressure. Its progenitor, based on statistical predictions of the collective motion of particles from their microscopic behavior, is the field of statistical thermodynamics (or statistical mechanics), a branch of statistical physics.^[2][3][4] Historically, thermodynamics developed out of need to increase the efficiency of early steam engines.^[5]

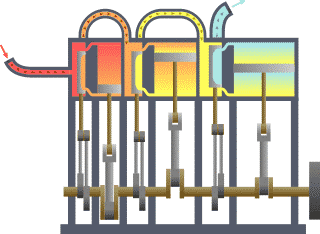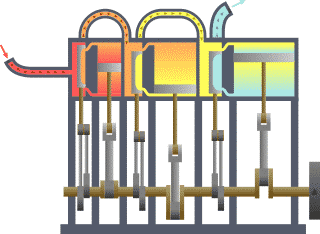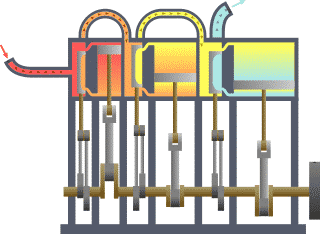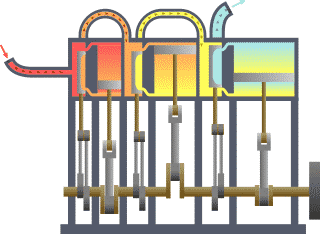
Typical thermodynamic system, showing input from a heat source (boiler) on the left and output to a heat sink (condenser) on the right. Work is extracted, in this case by a series of pistons.

Contents 1 Introduction 2 Developments 3 The Four Laws 4 Potentials 5 System models 6 Conjugate variables 7 Instrumentation 8 States & processes 9 See also 9.1 Applied fields 9.2 Other 9.3 Wikibooks 10 References 11 Further reading 12 External links

Introduction

Thermodynamic equations
Laws of thermodynamics
Conjugate variables
Thermodynamic potential
Material properties
Maxwell relations
Bridgman's equations
Exact differential
Table of thermodynamic equations
edit

The starting point for most thermodynamic considerations are the laws of thermodynamics, which postulate that energy can be exchanged between physical systems as heat or work.^[6] They also postulate the existence of a quantity named entropy, which can be defined for any isolated system that is in thermodynamic equilibrium.^[7] In thermodynamics, interactions between large ensembles of objects are studied and categorized. Central to this are the concepts of system and surroundings. A system is composed of particles, whose average motions define its properties, which in turn are related to one another through equations of state. Properties can be combined to express internal energy and thermodynamic potentials, which are useful for determining conditions for equilibrium and spontaneous processes.
With these tools, the usage of thermodynamics describes how systems respond to changes in their surroundings. This can be applied to a wide variety of topics in science and engineering, such as engines, phase transitions, chemical reactions, transport phenomena, and even black holes. The results of thermodynamics are essential for other fields of physics and for chemistry, chemical engineering, aerospace engineering, mechanical engineering, cell biology, biomedical engineering, materials science, and economics to name a few.^[8][9]

Developments

Sadi Carnot (1796-1832), the father of thermodynamics

Main article: History of thermodynamics

The history of thermodynamics as a scientific discipline generally begins with Otto von Guericke who, in 1650, built and designed the world's first vacuum pump and demonstrated a vacuum using his Magdeburg hemispheres. Guericke was driven to make a vacuum in order to disprove Aristotle's long-held supposition that 'nature abhors a vacuum'. Shortly after Guericke, the Irish physicist and chemist Robert Boyle had learned of Guericke's designs and, in 1656, in coordination with English scientist Robert Hooke, built an air pump.^[10] Using this pump, Boyle and Hooke noticed a correlation between pressure, temperature, and volume. In time, Boyle's Law was formulated, which states that pressure and volume are inversely proportional. Then, in 1679, based on these concepts, an associate of Boyle's named Denis Papin built a bone digester, which was a closed vessel with a tightly fitting lid that confined steam until a high pressure was generated.
Later designs implemented a steam release valve that kept the machine from exploding. By watching the valve rhythmically move up and down, Papin conceived of the idea of a piston and a cylinder engine. He did not, however, follow through with his design. Nevertheless, in 1697, based on Papin's designs, engineer Thomas Savery built the first engine. Although these early engines were crude and inefficient, they attracted the attention of the leading scientists of the time. Their work led 127 years later to Sadi Carnot, the "father of thermodynamics", who, in 1824, published Reflections on the Motive Power of Fire, a discourse on heat, power, and engine efficiency. The paper outlined the basic energetic relations between the Carnot engine, the Carnot cycle, and Motive power. It marked the start of thermodynamics as a modern science.^[3]. The term thermodynamics was coined by James Joule in 1849 to designate the science of relations between heat and power.^[3] By 1858, "thermo-dynamics", as a functional term, was used in William Thomson's paper An Account of Carnot's Theory of the Motive Power of Heat.^[11] The first thermodynamic textbook was written in 1859 by William Rankine, originally trained as a physicist and a civil and mechanical engineering professor at the University of Glasgow.^[12]
Classical thermodynamics is the early 1800s variation of the original thermodynamics, concerned with thermodynamic states and properties, such as energy, work and heat, and with the laws of thermodynamics, all lacking an atomic interpretation.
In precursory form, classical thermodynamics derives from chemist Robert Boyle’s 1662 postulate that the pressure P of a given quantity of gas varies inversely as its volume V at constant temperature; i.e. in equation form: PV = k, a constant. From here, a semblance of a thermo-science began to develop with the construction of the first successful atmospheric steam engines in England by Thomas Savery in 1697 and Thomas Newcomen in 1712. The first and second laws of thermodynamics emerged simultaneously in the 1850s, primarily out of the works of William Rankine, Rudolf Clausius, and William Thomson (Lord Kelvin).
With the development of atomic and molecular theories in the late 1800s and early 1900s, thermodynamics was given a molecular interpretation. This field, called statistical mechanics or statistical thermodynamics, relates the microscopic properties of individual atoms and molecules to the macroscopic or bulk properties of materials that can be observed in everyday life, thereby explaining thermodynamics as a natural result of statistics and mechanics (classical and quantum) at the microscopic level. The statistical approach is in contrast to classical thermodynamics, which is a more phenomenological approach that does not include microscopic details. The foundations of statistical thermodynamics were set out by physicists such as James Clerk Maxwell, Ludwig Boltzmann, Max Planck, Rudolf Clausius and J. Willard Gibbs.
Chemical thermodynamics is the study of the interrelation of energy with chemical reactions or with a physical change of state within the confines of the laws of thermodynamics. During the years 1873-76 the American mathematical physicist Josiah Willard Gibbs published a series of three papers, the most famous being On the Equilibrium of Heterogeneous Substances, in which he showed how thermodynamic processes could be graphically analyzed, by studying the energy, entropy, volume, temperature and pressure of the thermodynamic system in such a manner, one can determine if a process would occur spontaneously.^[13] During the early 20th century, chemists such as Gilbert N. Lewis, Merle Randall, and E. A. Guggenheim began to apply the mathematical methods of Gibbs to the analysis of chemical processes.^[14]

The Four Laws

Main article: Laws of thermodynamics

The present article is focused on classical thermodynamics, which is focused on systems in thermodynamic equilibrium. It is wise to distinguish classical thermodynamics from non-equilibrium thermodynamics, which is concerned with systems that are not in thermodynamic equilibrium.
In thermodynamics, there are four laws that do not depend on the details of the systems under study or how they interact. Hence these laws are very generally valid, can be applied to systems about which one knows nothing other than the balance of energy and matter transfer. Examples of such systems include Einstein's prediction, around the turn of the 20th century, of spontaneous emission, and ongoing research into the thermodynamics of black holes.
These four laws are:

• Zeroth law of thermodynamics, about thermal equilibrium:

If two thermodynamic systems are separately in thermal equilibrium with a third, they are also in thermal equilibrium with each other.

If we grant that all systems are (trivially) in thermal equilibrium with themselves, the Zeroth law implies that thermal equilibrium is an equivalence relation on the set of thermodynamic systems. This law is tacitly assumed in every measurement of temperature. Thus, if we want to know if two bodies are at the same temperature, it is not necessary to bring them into contact and to watch whether their observable properties change with time.^[15]

This law was considered so obvious it was added as a virtual after thought, hence the designation Zeroth, rather than Fourth. In short, if the heat energy of material A is equal to the heat energy of material B, and B is equal to the heat energy of material C. then A and C must also be equal.

• First law of thermodynamics, about the conservation of energy:

The change in the internal energy of a closed thermodynamic system is equal to the sum of the amount of heat energy supplied to or removed from the system and the work done on or by the system or we can say " In an isolated system the heat is constant".

• Second law of thermodynamics, about entropy:

The total entropy of any isolated thermodynamic system always increases over time, approaching a maximum value or we can say " in an isolated system, the entropy never decreases". Another way to phrase this: Heat cannot spontaneously flow from a colder location to a hotter area - work is required to achieve this.

• Third law of thermodynamics, about the absolute zero of temperature:

As a system asymptotically approaches absolute zero of temperature all processes virtually cease and the entropy of the system asymptotically approaches a minimum value; also stated as: "the entropy of all systems and of all states of a system is zero at absolute zero" or equivalently "it is impossible to reach the absolute zero of temperature by any finite number of processes". Absolute zero, at which all activity would stop if it were possible to happen, is −273.15 °C (degrees Celsius), or −459.67 °F (degrees Fahrenheit) or 0 K (kelvins, formerly sometimes degrees absolute).

See also: Bose–Einstein condensate and negative temperature.

Potentials

Main article: Thermodynamic potentials

As can be derived from the energy balance equation (or Burks' equation) on a thermodynamic system there exist energetic quantities called thermodynamic potentials, being the quantitative measure of the stored energy in the system. The five most well known potentials are:

Internal energy
Helmholtz free energy
Enthalpy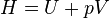
Gibbs free energy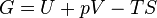
Grand potential

Other thermodynamic potentials can be obtained through Legendre transformation. Potentials are used to measure energy changes in systems as they evolve from an initial state to a final state. The potential used depends on the constraints of the system, such as constant temperature or pressure. Internal energy is the internal energy of the system, enthalpy is the internal energy of the system plus the energy related to pressure-volume work, and Helmholtz and Gibbs energy are the energies available in a system to do useful work when the temperature and volume or the pressure and temperature are fixed, respectively.

System models

Main article: Thermodynamic system

An important concept in thermodynamics is the “system”. Everything in the universe except the system is known as surroundings. A system is the region of the universe under study. A system is separated from the remainder of the universe by a boundary which may be imaginary or not, but which by convention delimits a finite volume. The possible exchanges of work, heat, or matter between the system and the surroundings take place across this boundary. Boundaries are of four types: fixed, moveable, real, and imaginary.
Basically, the “boundary” is simply an imaginary dotted line drawn around a volume of something when there is going to be a change in the internal energy of that something. Anything that passes across the boundary that effects a change in the internal energy of the something needs to be accounted for in the energy balance equation. That something can be the volumetric region surrounding a single atom resonating energy, such as Max Planck defined in 1900; it can be a body of steam or air in a steam engine, such as Sadi Carnot defined in 1824; it can be the body of a tropical cyclone, such as Kerry Emanuel theorized in 1986 in the field of atmospheric thermodynamics; it could also be just one nuclide (i.e. a system of quarks) as some are theorizing presently in quantum thermodynamics.
For an engine, a fixed boundary means the piston is locked at its position; as such, a constant volume process occurs. In that same engine, a moveable boundary allows the piston to move in and out. For closed systems, boundaries are real while for open system boundaries are often imaginary. There are five dominant classes of systems:

1. Isolated Systems – matter and energy may not cross the boundary
2. Adiabatic Systems – heat must not cross the boundary
3. Diathermic Systems - heat may cross boundary
4. Closed Systems – matter may not cross the boundary
5. Open Systems – heat, work, and matter may cross the boundary (often called a control volume in this case)

As time passes in an isolated system, internal differences in the system tend to even out and pressures and temperatures tend to equalize, as do density differences. A system in which all equalizing processes have gone practically to completion, is considered to be in a state of thermodynamic equilibrium.
In thermodynamic equilibrium, a system's properties are, by definition, unchanging in time. Systems in equilibrium are much simpler and easier to understand than systems which are not in equilibrium. Often, when analysing a thermodynamic process, it can be assumed that each intermediate state in the process is at equilibrium. This will also considerably simplify the situation. Thermodynamic processes which develop so slowly as to allow each intermediate step to be an equilibrium state are said to be reversible processes.




Conjugate variables

Main article: Conjugate variables (thermodynamics)

The central concept of thermodynamics is that of energy, the ability to do work. By the First Law, the total energy of a system and its surroundings is conserved. Energy may be transferred into a system by heating, compression, or addition of matter, and extracted from a system by cooling, expansion, or extraction of matter. In mechanics, for example, energy transfer equals the product of the force applied to a body and the resulting displacement.
Conjugate variables are pairs of thermodynamic concepts, with the first being akin to a "force" applied to some thermodynamic system, the second being akin to the resulting "displacement," and the product of the two equalling the amount of energy transferred. The common conjugate variables are:

• Pressure-volume (the mechanical parameters);
• Temperature-entropy (thermal parameters);
• Chemical potential-particle number (material parameters).

Instrumentation

Main article: Thermodynamic instruments

There are two types of thermodynamic instruments, the meter and the reservoir. A thermodynamic meter is any device which measures any parameter of a thermodynamic system. In some cases, the thermodynamic parameter is actually defined in terms of an idealized measuring instrument. For example, the zeroth law states that if two bodies are in thermal equilibrium with a third body, they are also in thermal equilibrium with each other. This principle, as noted by James Maxwell in 1872, asserts that it is possible to measure temperature. An idealized thermometer is a sample of an ideal gas at constant pressure. From the ideal gas law pV=nRT, the volume of such a sample can be used as an indicator of temperature; in this manner it defines temperature. Although pressure is defined mechanically, a pressure-measuring device, called a barometer may also be constructed from a sample of an ideal gas held at a constant temperature. A calorimeter is a device which is used to measure and define the internal energy of a system.
A thermodynamic reservoir is a system which is so large that it does not appreciably alter its state parameters when brought into contact with the test system. It is used to impose a particular value of a state parameter upon the system. For example, a pressure reservoir is a system at a particular pressure, which imposes that pressure upon any test system that it is mechanically connected to. The Earth's atmosphere is often used as a pressure reservoir.
It is important that these two types of instruments are distinct. A meter does not perform its task accurately if it behaves like a reservoir of the state variable it is trying to measure. If, for example, a thermometer were to act as a temperature reservoir it would alter the temperature of the system being measured, and the reading would be incorrect. Ideal meters have no effect on the state variables of the system they are measuring.

States & processes

Main article: Thermodynamic state

Main article: Thermodynamic processes

When a system is at equilibrium under a given set of conditions, it is said to be in a definite state. The thermodynamic state of the system can be described by a number of intensive variables and extensive variables. The properties of the system can be described by an equation of state which specifies the relationship between these variables. State may be thought of as the instantaneous quantitative description of a system with a set number of variables held constant.
A thermodynamic process may be defined as the energetic evolution of a thermodynamic system proceeding from an initial state to a final state. Typically, each thermodynamic process is distinguished from other processes, in energetic character, according to what parameters, as temperature, pressure, or volume, etc., are held fixed. Furthermore, it is useful to group these processes into pairs, in which each variable held constant is one member of a conjugate pair. The seven most common thermodynamic processes are shown below:

1. An isobaric process occurs at constant pressure.
2. An isochoric process, or isometric/isovolumetric process, occurs at constant volume.
3. An isothermal process occurs at a constant temperature.
4. An adiabatic process occurs without loss or gain of energy by heat.
5. An isentropic process (reversible adiabatic process) occurs at a constant entropy.
6. An isenthalpic process occurs at a constant enthalpy.
7. A steady state process occurs without a change in the internal energy of a system.

See also

Physics portal

Applied fields

Atmospheric thermodynamics Biological thermodynamics Black hole thermodynamics Chemical thermodynamics Classical thermodynamics

Equilibrium thermodynamics Maximum entropy thermodynamics Non-equilibrium thermodynamics Philosophy of thermal and statistical physics

Psychrometrics Quantum thermodynamics Statistical thermodynamics Thermoeconomics

Other

Lists and timelines:

• List of important publications in thermodynamics
• List of textbooks in statistical mechanics
• List of thermal conductivities
• List of thermodynamic properties
• Table of thermodynamic equations
• Timeline of thermodynamics, statistical mechanics, and random processes

Thermodynamic:

Boundary Component Conjugate variables Temperature / Entropy Pressure / Volume (Stress / Strain) Chemical potential / Particle number Constant: Avogadro's NA Boltzmann k Ideal gas R Stefan-Boltzmann σ Critical line Cycle External combustion engine Internal combustion engine Atkinson Bell Coleman Brayton Carnot Combined Diesel Ericsson Hampson-Linde Heat engine Carnot HEHC Hot air engine Heat pump & refrigeration Kalina Kleemenko Lenoir Miller Mixed/Dual Otto Rankine Regenerative Siemens Stirling Stoddard Ensemble Canonical Grand canonical Isoenthalpic-isobaric Isothermal-isobaric Microcanonical Equations Boltzmann Bridgman Churchill-Bernstein Clausius-Clapeyron relation Debye-Hückel Equation of state Exact differential Gibbs-Duhem Gibbs-Helmholtz Green-Kubo relations Maxwell relations Onsager reciprocal relations

Equilibrium Chemical Dynamic Local Phase History Instruments Barometer Calorimeter Dynamometer Thermometer Laws: Zeroth First Second Third Charles's Dulong-Petit Fundamental relation Gas laws Ideal gas Joule's Onsager reciprocal relations Stefan-Boltzmann Limit Material properties Bulk modulus K Compressibility β Specific heat capacity c Thermal expansion α Potential Internal energy Entropy Gibbs free energy Grand Helmholtz free energy Process Adiabatic Isenthalpic Isentropic Isobaric Isochoric Isothermal Quasistatic Spontaneous Steady state State Excited Function Ground Standard Stationary Steady System Closed Dissipative Isolated Temperature Negative Range

Variable: Chemical potential μ Density Energy Conservation of Conversion efficiency Electrical Free Gibbs free G Helmholtz free A Internal U Kinetic Potential Specific Enthalpy H Entropy S & information theory As energy dispersal Introduction to Residual Shannon Statistical Exergy Efficiency Mass Mole (unit) Particle number N Pressure P Temperature T Volume V Work W Mechanical Theorem: Carnot's Clausius Equipartition Bolzmann's H Nernst heat Virial

Other Related Topics

Heat: Critical heat flux Heat of combustion Heat transfer Convective Latent heat Mechanical equivalent Theory of heat Volumetric heat capacity Thermal: Analysis Conductivity Contact Efficiency Energy Equilibrium Expansion Negative Mass Motion Radiation Science

Physical chemistry: Autocatalytic reactions and order creation Boiling point Calorimetry Chemical energetics Chemical kinetics Endergonic reaction Endothermic Exothermic Gibbs phase rule Melting point Phase diagram Calphad Phase transition Thermodynamic databases for pure substances Triple point Vapor-liquid equilibrium

Statistical Mechanics: Boltzmann distribution Boltzmann distribution law Boltzmann factor Bose-Einstein condensate Bose-Einstein statistics Brownian motion Configuration integral Degeneracy Degrees of freedom Fermi-Dirac statistics Fluctuations Gibbs paradox Ideal gas Irreversibility Kinetic theory Macrostate Maxwell-Boltzmann statistics Microstate Molecular chaos Partition function Thermoelectricity: Nernst effect Peltier effect Seebeck effect Thermionic emission Thermoelectric effect Thermoelectricity Thermogenerator Thermophotovoltaic Thermopower Thomson effect

Sundry: Absolute zero Arrow of time Black body Dissipation Ettingshausen effect Extensive quantity Intensive quantity Legendre transformation Loschmidt's paradox Mass-energy equivalence Physical information Piezoelectric effect Pressure volume diagram Pyroelectric effect Quality of a fluid Refrigeration Gas asbsorption Cycle Thermoelectric cooling Vapor compression Standard conditions for temperature and pressure Thermodynamic paradox T-symmetry Two dimensional gas

Wikibooks

• Engineering Thermodynamics
• Entropy for Beginners

References

1. ^ Oxford American Dictionary
2. ^ Enrico Fermi (1956). Thermodynamics. Courier Dover Publications. pp. (ix). ISBN 048660361X. OCLC 230763036 54033021. http://books.google.com/books?id=VEZ1ljsT3IwC&printsec=frontcover&dq=thermodynamics&lr=&as_brr=0&sig=ACfU3U24MHXNw_T3n2dj1QHRnPKxNyX7-g#PPP11,M1. 
3. ^ ^{a b c} Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6. OCLC 123283342 38073404. 
4. ^ Clark, John, O.E. (2004). The Essential Dictionary of Science. Barnes & Noble Books. ISBN 0-7607-4616-8. OCLC 58732844 63473130. 
5. ^ Clausius, Rudolf (1850). On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff's Annalen der Physick, LXXIX (Dover Reprint). ISBN 0-486-59065-8. 
6. ^ Van Ness, H.C. (1969). Understanding Thermodynamics. Dover Publications, Inc.. ISBN 0-486-63277-6. OCLC 8846081. 
7. ^ Dugdale, J.S. (1998). Entropy and its Physical Meaning. Taylor and Francis. ISBN 0-7484-0569-0. OCLC 36457809. 
8. ^ Smith, J.M.; Van Ness, H.C., Abbott, M.M. (2005). Introduction to Chemical Engineering Thermodynamics. McGraw Hill. ISBN 0-07-310445-0. OCLC 56491111. 
9. ^ Haynie, Donald, T. (2001). Biological Thermodynamics. Cambridge University Press. ISBN 0-521-79549-4. OCLC 43993556. 
10. ^ Partington, J.R. (1989). A Short History of Chemistry. Dover. ISBN 0-486-65977-1. OCLC 19353301. 
11. ^ Kelvin, William T. (1849) "An Account of Carnot's Theory of the Motive Power of Heat - with Numerical Results Deduced from Regnault's Experiments on Steam." Transactions of the Edinburg Royal Society, XVI. January 2. Scanned Copy
12. ^ Cengel, Yunus A.; Boles, Michael A. (2005). Thermodynamics - an Engineering Approach. McGraw-Hill. ISBN 0-07-310768-9. 
13. ^ Gibbs, Willard (1993). The Scientific Papers of J. Willard Gibbs, Volume One: Thermodynamics. Ox Bow Press. ISBN 0-918024-77-3. OCLC 27974820. 
14. ^ Lewis, Gilbert N.; Randall, Merle (1923). Thermodynamics and the Free Energy of Chemical Substances. McGraw-Hill Book Co. Inc.. 
15. ^ Moran, Michael J. and Howard N. Shapiro, 2008. Fundamentals of Engineering Thermodynamics. 6th ed. Wiley and Sons: 16.

Further reading

• Goldstein, Martin, and Inge F. (1993). The Refrigerator and the Universe. Harvard University Press. ISBN 0-674-75325-9. OCLC 32826343.  A nontechnical introduction, good on historical and interpretive matters.
• Kazakov, Andrei (July-August 2008). "Web Thermo Tables – an On-Line Version of the TRC Thermodynamic Tables". Journal of Research of the National Institutes of Standards and Technology 113 (4): 209–220. http://nvl-i.nist.gov/pub/nistpubs/jres/113/4/V113.N04.A03.pdf. 

The following titles are more technical:

• Cengel, Yunus A., & Boles, Michael A. (2002). Thermodynamics - an Engineering Approach. McGraw Hill. ISBN 0-07-238332-1. OCLC 45791449 52263994 57548906. 
• Dunning-Davies, Jeremy (1997). Concise Thermodynamics: Principles and Applications. Horwood Publishing. ISBN 1-8985-6315-2. OCLC 36025958 60273489. 
• Kroemer, Herbert & Kittel, Charles (1980). Thermal Physics. W. H. Freeman Company. ISBN 0-7167-1088-9. OCLC 32932988 48236639 5171399. 

External links

Wikiquote has a collection of quotations related to: Thermodynamics

• Thermodynamics Data & Property Calculation Websites
• Thermodynamics Educational Websites
• Thermodynamics at ScienceWorld
• History of Thermodynamics
• Shakespeare & Thermodynamics
• Biochemistry Thermodynamics
• Thermodynamics and Statistical Mechanics
• Free Steam Tables Online calculator based on IAPWS-IF97
• Engineering Thermodynamics - A Graphical Approach