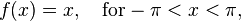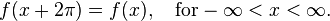Invented by a Jewish chap in the WWII Buchenwald Death Camp, Curtas were widely considered the best portable calculators available until they were displaced by electronic calculators in the 1970s.
I just went to e-Bay and they're being offered for sale in a price range from $348 to $1500.
The
Curta is a small, hand-cranked mechanical
calculator introduced in 1948. It has an extremely compact design: a small cylinder that fits in the palm of the hand. It can be used to perform addition, subtraction, multiplication, division, and —with more difficulty— square roots and other operations.
The Curta's design is a descendant of
Gottfried Leibniz's
Stepped Reckoner and
Thomas's
Arithmometer, accumulating values on
cogs, which are added or complemented by a
stepped drum mechanism.
History of the Invention
The Curta was conceived by
Curt Herzstark (1902–1988) in the 1930s in Vienna. By 1938, he had filed a key patent, covering his complemented stepped drum, Deutsches Reichspatent (German Empire Patent) No. 747073. This single drum replaced the multiple drums, typically around 10 or so, of contemporary calculators, and it enabled not only addition, but subtraction through
nines complement math, essentially subtracting by adding. The nines' complement math breakthrough eliminated the significant mechanical complexity created when "borrowing" during subtraction. This drum would prove to be the key to the small, hand-held mechanical calculator the Curta would become.
His work on the pocket calculator stopped in 1938 when the Nazis forced him and his company to concentrate on manufacturing measuring instruments and distance gauges for the German army.
Herzstark, the son of a Catholic mother but Jewish father, was taken into custody in 1943, eventually finding himself at the
Buchenwald concentration camp. Ironically, it was in the concentration camp that he was encouraged to continue his earlier research: "While I was imprisoned inside [Buchenwald] I had, after a few days, told the [people] in the work production scheduling department of my ideas. The head of the department, Mr. Munich said, 'See, Herzstark, I understand you've been working on a new thing, a small calculating machine. Do you know, I can give you a tip. We will allow you to make and draw everything. If it is really worth something, then we will give it to the Führer as a present after we win the war. Then, surely, you will be made an Aryan.' For me, that was the first time I thought to myself, my God, if you do this, you can extend your life. And then and there I started to draw the CURTA, the way I had imagined it."
[1]Herzstark worked furiously to move his invention from his knowing how to build the device "in principle"
[1] to concise working drawings for a manufacturable device.
The department head's celebration plan didn't work out, but Herzstark's construction plans did: Between April 11, 1945, when Buchenwald was liberated by the Americans, and the following November, Herzstark was, after making only a few "detailed improvements"
[1] to the design, able to locate a factory in Sommertal, near
Weimar, where machinists were skilled enough to work at the necessary level of precision, and walk away with three working models of the calculator.
The Russians had arrived in July, and Hertstark feared being sent to Russia, so, later that same month, he fled to Austria. He began to look for financial backers, at the same time filing continuing patents as well as several additional patents to protect his work. The Prince of
Liechtenstein eventually showed interest in the manufacture of the device, and soon a newly-formed company, Contina AG Mauren, (aka, Contina Ltd Mauren) began production in Liechtenstein.
It wasn't long before the money men, apparently having gotten from him all they thought they needed, contrived to force him out by reducing the value of all existing stock to zero, including his one-third interest in the company. These were the same money men who, earlier, had elected not to transfer ownership of the Herzstark's patents to the company, so that, should anyone sue, they'd be suing Herzstark, not the company, thereby protecting themselves at Herzstark's expense. This ploy now backfired: Without the patent rights, they could manufacture nothing. Herzstark was able to negotiate a new agreement, and money continued to flow to him.
Curtas were widely considered the best portable calculators available until they were displaced by electronic calculators in the 1970s. Herzstark continued to make money from his invention until that time, although, like many inventors before him, he was not among those who profited the most from his invention. The Curta, however, lives on, being a highly-popular collectible, with thousands of machines working just as smoothly as they did 40, 50, and 60 years ago when they were manufactured.
[1][2][3]Description and use
Numbers are entered using slides (one slide per digit) on the side of the device. The revolution counter and result counter appear on the top. A single turn of the crank adds the input number to the result counter, at any position, and increments the revolution counter accordingly. Pulling the crank upwards slightly before turning it performs a subtraction instead of an addition. Multiplication, division, and other functions require a series of crank and carriage-shifting operations.
The Curta was affectionately known as the "pepper grinder" or "peppermill" due to its shape and means of operation. It was also termed the "math grenade", due to its superficial resemblance to a certain type of hand grenade.
Curta Type I and Type II
The Type I Curta has 8 digits for data entry (known as "setting sliders"), a 6-digit revolution counter, and an 11-digit result counter. According to the advertising literature, it weighs only 8 ounces (about 230 grams). Serial number 70154, produced in 1969, weighs 245 grams.
The larger Type II Curta, introduced in 1954, has 11 digits for data entry (known as "setting sliders"), an 8-digit revolution counter, and a 15-digit result counter. It weighs 13.15 ounces or 373 grams, based on weighing serial number 550973, produced in early 1966.
An estimated 140,000 Curta calculators were made (80,000 Type I and 60,000 Type II). According to Curt Herzstark, the last Curta was produced in 1972.
[1]Gallery
A partially disassembled Curta calculator, showing the digit slides and the stepped drum behind them.
Curta Type I calculator showing view from top.
Curta Type I calculator showing view from bottom.
Use in car rallies
The Curta was popular among contestants in
sports car rallies during the 1960s, 1970s and into the 1980s. Even after the introduction of the electronic calculator for other purposes, they were used in time-speed-distance (TSD) rallies to aid in computation of times to checkpoints, distances off-course, etc., since the early electronic calculators did not fare well with the bounces and jolts of rally racing.
[citation needed]Contestants who used such calculators were often called "Curta-crankers" by those who were limited to paper and pencil, or who used computers linked to the car's wheels.
[citation needed]Curta calculators contributed to the saying when describing the process of calculating, "Cranking out the answer."
[citation needed]Use by pilots
The Curta was also favored by both commercial and general-aviation pilots, before the advent of electronic calculators, because of both its precision and the user's ability to confirm the accuracy of his or her manipulations via the revolution counter. Because calculations such as weight and balance are a matter of life and death, precise results free of pilot error are essential.
The real cost of a Curta
While only 3% of Curtas were returned to the factory because of repairs under warranty
[1], a small, but significant stream returned the Curta in pieces. Many purchasers attempted to disassemble the Curta. Reassembling the machine was more difficult, as assembly required intimate knowledge of the orientation and installation order for each part and sub-assembly. Many identical looking parts, each with slightly different dimensions, required test fitting and selection as well as special tools to adjust tolerances. One chagrined owner, on showing up to the dealer to retrieve his $600 Curta, now reassembled for an additional $300, was told, "don't feel bad. Curtas really cost $900. Everyone takes them apart."
[4]The Curta in print
Lastly, the Curta is on the Popular Science magazine list of top 100 pieces of retro technology.
References
External links


![\begin{align}
f(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty}\left[a_n\cos\left(nx\right)+b_n\sin\left(nx\right)\right] \\
&=2\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n} \sin(nx), \quad \mathrm{for} \quad x - \pi \notin 2 \pi \mathbf{Z}.
\end{align}](http://upload.wikimedia.org/math/c/0/6/c06c0f50fec40edaf0ab2eb64841e9bf.png)


![(S_N f)(x) = \frac{a_0}{2} + \sum_{n=1}^N \, [a_n \cos(nx) + b_n \sin(nx)], \quad N \ge 0.](http://upload.wikimedia.org/math/4/e/8/4e86d41e4f279575401346647b9abf63.png)
![\frac{a_0}{2} + \sum_{n=1}^\infty \, [a_n \cos(nx) + b_n \sin(nx)]](http://upload.wikimedia.org/math/f/7/1/f712dc7dc49203f6412ed644d1426ab1.png)