What do Bach's compositions, Rubik's Cube, the way we choose our mates, and the physics of subatomic particles have in common? All are grounded by laws of symmetry, which elegantly unify scientific and artistic principles. Yet the mathematical language of symmetry - known as group theory - did not emerge from the study of symmetry at all, but from an equation that couldn't be solved.
For thousands of years mathematicians solved progressively more difficult algebraic equations, until they encountered the quintic equation, which resisted solution for three centuries. Working independently, two great prodigies ultimately proved that the quintic cannot be solved by a simple formula. Those geniuses, a Norwegian named Niels Henrik Abel and a romantic Frenchman named Evariste Galois, both died tragically young. Their incredible labor, however, produced the origins of group theory.
The first extensive, popular account of the mathematics of symmetry and order, The Equation That Couldn't Be Solved, by Mario Livio, is told now through abstract formulas but in a beautifully written and dramatic account of the lives and the work of some of the greatest and most intriguing mathematicians in history.
The blurb for the aforementioned book.
From Wikipedia:
In mathematics, a quintic function is a function of the form
where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero. In other words, a quintic function is a polynomial of degree five.
Setting ƒ(x) = 0 and assuming a ≠ 0 produces a quintic equation of the form:
If a is zero but one of the other coefficients is non-zero, the equation is classified as either a quartic equation, cubic equation, quadratic equation or linear equation.
Because they have an odd degree, normal quintic functions appear similar to normal cubic functions when graphed, except they may possess an additional local maximum and local minimum each. The derivative of a quintic function is a quartic function.
Contents[hide]
|
Finding the roots of a polynomial—values of x which satisfy such an equation—in the rational case given its coefficients has been a prominent mathematical problem.
Solving linear, quadratic, cubic and quartic equations by factorization into radicals is fairly straightforward, no matter whether the roots are rational or irrational, real or complex; there are also formulae that yield the required solutions. However, there is no formula for general quintic equations over the rationals in terms of radicals; this is known as the Abel–Ruffini theorem, first published in 1824, which was one of the first applications of group theory in algebra. This result also holds for equations of higher degrees. An example quintic whose roots cannot be expressed by radicals is x5 − x + 1 = 0. This quintic is in Bring–Jerrard normal form.
As a practical matter, exact analytic solutions for polynomial equations are often unnecessary, and so numerical methods such as Laguerre's method or the Jenkins-Traub method are probably the best way of obtaining solutions to general quintics and higher degree polynomial equations that arise in practice. However, analytic solutions are sometimes useful for certain applications, and many mathematicians have tried to develop them.
]Solvable quintics
Some fifth-degree equations can be solved by factorizing into radicals, for example  , which can be written as
, which can be written as  or
or  which has
which has ![\sqrt[5]{2}\,](http://upload.wikimedia.org/math/e/7/1/e71f9122c1144b7d9d5a387fb5ff9d56.png) as solution. Other quintics like
as solution. Other quintics like  cannot be solved by radicals. Évariste Galois developed techniques for determining whether a given equation could be solved by radicals which gave rise togroup theory and Galois theory. Applying these techniques, Arthur Cayley has found a general criterion for determining whether any given quintic is solvable.[1] This criterion is the following.[2]
cannot be solved by radicals. Évariste Galois developed techniques for determining whether a given equation could be solved by radicals which gave rise togroup theory and Galois theory. Applying these techniques, Arthur Cayley has found a general criterion for determining whether any given quintic is solvable.[1] This criterion is the following.[2]
 , which can be written as
, which can be written as  or
or  which has
which has ![\sqrt[5]{2}\,](http://upload.wikimedia.org/math/e/7/1/e71f9122c1144b7d9d5a387fb5ff9d56.png) as solution. Other quintics like
as solution. Other quintics like  cannot be solved by radicals. Évariste Galois developed techniques for determining whether a given equation could be solved by radicals which gave rise togroup theory and Galois theory. Applying these techniques, Arthur Cayley has found a general criterion for determining whether any given quintic is solvable.[1] This criterion is the following.[2]
cannot be solved by radicals. Évariste Galois developed techniques for determining whether a given equation could be solved by radicals which gave rise togroup theory and Galois theory. Applying these techniques, Arthur Cayley has found a general criterion for determining whether any given quintic is solvable.[1] This criterion is the following.[2]Given the equation
- ax5 + bx4 + cx3 + dx2 + ex + f = 0,
the Tschirnhaus transformation 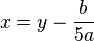 gives the equation
gives the equation
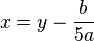 gives the equation
gives the equation- y5 + py3 + qy2 + ry + s = 0,
where
Both equations are solvable by radicals if and only if either they are factorisable in equations of lower degrees with rational coefficients or the polynomial P2 − 210zΔ, named Cayley resolvent, has a rational root in z, where
- P = z3 − z2(20r + 3p2) − z(8p2r − 16pq2 − 240r2 + 400sq − 3p4)
- − p6 + 28p4r − 16p3q2 − 176p2r2 − 80p2sq + 224prq2 − 64q4
- + 4000ps2 + 320r3 − 1600rsq
and
- Δ = − 128p2r4 + 3125s4 − 72p4qrs + 560p2qr2s + 16p4r3 + 256r5 + 108p5s2
- − 1600qr3s + 144pq2r3 − 900p3rs2 + 2000pr2s2 − 3750pqs3 + 825p2q2s2
- + 2250q2rs2 + 108q5s − 27q4r2 − 630pq3rs + 16p3q3s − 4p3q2r2
In 1888, George Paxton Young[3] described how to solve a solvable quintic equation, without providing an explicit formula; Lazard (2004) writes out the three-page formula.
During the second half of 19th century, John Stuart Glashan, George Paxton Young, and Carl Runge have also found that any irreducible quintic with rational coefficients in Bring-Jerrard form,
is solvable by radicals if and only if either a = 0 or it is of the following form:
where μ and ν are rational. In 1994, Blair Spearman and Kenneth S. Williams gave an alternative,
The relationship between the 1885 and 1994 parameterizations can be seen by defining the expression
where
and using the negative case of the square root yields, after scaling variables, the first parametrization while the positive case gives the second. It is then a necessary (but not sufficient) condition that the irreducible solvable quintic
with rational coefficients must satisfy the simple quadratic curve
for some rational a,y.
The substitution c = − m / l5, e = 1 / l in Spearman-Williams parameterization allows to not exclude the special case a = 0, giving the following result:
If a and b are rational numbers, the equation x5 + ax + b = 0 is solvable by radicals if either its left hand side is a product of polynomials of degree less than 5 with rational coefficients or there exist two rational numbers l and m such that
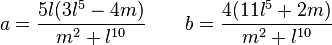 .
.
[Examples of solvable quintics
A quintic is solvable using radicals if the Galois group of the quintic (which is a subgroup of the symmetric group S(5) of permutations of a five element set) is a solvable group. In this case the form of the solutions depends on the structure of this Galois group.
A simple example is given by the equation 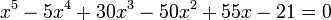 , whose Galois group is the group F(5) generated by the permutations "(1 2 3 4 5)" and "(1 2 4 3)"; the only real solution is
, whose Galois group is the group F(5) generated by the permutations "(1 2 3 4 5)" and "(1 2 4 3)"; the only real solution is
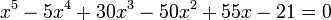 , whose Galois group is the group F(5) generated by the permutations "(1 2 3 4 5)" and "(1 2 4 3)"; the only real solution is
, whose Galois group is the group F(5) generated by the permutations "(1 2 3 4 5)" and "(1 2 4 3)"; the only real solution isHowever, for other solvable Galois groups, the form of the roots can be much more complex. For example, the equation  has Galois group D(5) generated by "(1 2 3 4 5)" and "(1 4)(2 3)" and the solution requires more symbols to write. Define,
has Galois group D(5) generated by "(1 2 3 4 5)" and "(1 4)(2 3)" and the solution requires more symbols to write. Define,
 has Galois group D(5) generated by "(1 2 3 4 5)" and "(1 4)(2 3)" and the solution requires more symbols to write. Define,
has Galois group D(5) generated by "(1 2 3 4 5)" and "(1 4)(2 3)" and the solution requires more symbols to write. Define,then the only real solution 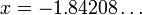 is exactly given by,
is exactly given by,
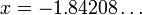 is exactly given by,
is exactly given by,Or equivalently,
where the yi are the four roots of the quartic equation,
In general, if an equation P(x) = 0 of prime degree p with rational coefficients is solvable in radicals, there is an auxiliary equation Q(y) = 0 of degree (p-1) also with rational coefficients that can be used to solve the former.
However, it is possible some of the roots of Q(y) = 0 are rational (like in the F(5) example given above) or some as zero, like the solvable DeMoivre quintic,
where the auxiliary equation has two zero roots and is essentially just the quadratic,
such that the five roots of the DeMoivre quintic are given by,
where ωk is any of the five 5th roots of unity. This can be easily generalized to construct a solvable septic and other odd degrees, not necessarily prime.
Here is a list of known solvable quintics:
There are infinitely many solvable quintics in Bring-Jerrard form which have been parameterized in preceding section.
Up to the scaling of the variable, there is exactly five solvable quintics of the shape x5 + ax2 + b, which are[4] (where s is a scaling factor):

- x5 − 100s3x2 − 1000s5
- x5 − 5s3x2 − 3s5
- x5 − 5s3x2 + 15s5
- x5 − 25s3x2 − 300s5
Paxton Young (1888) gave a number of examples, some of them being reducible, having a rational root:
| x5 − 10x3 − 20x2 − 1505x − 7412 | |
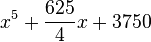 | |
 | |
| x5 + 20x3 + 20x2 + 30x + 10 | Solution: ![\sqrt[5]{2}-\sqrt[5]{2}^2+\sqrt[5]{2}^3-\sqrt[5]{2}^4](http://upload.wikimedia.org/math/5/7/d/57d93b74ea486324a4b75f8879f7e84c.png) |
| x5 + 320x2 − 1000x + 4288 | Reducible: −8 is a root |
| x5 + 40x2 − 69x + 108 | Reducible: −4 is a root |
| x5 − 20x3 + 250x − 400 | |
 | |
 | |
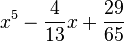 | |
 | |
| x5 + 110(5x3 + 60x2 + 800x + 8320) | |
| x5 − 20x3 − 80x2 − 150x − 656 | |
| x5 − 40x3 + 160x2 + 1000x − 5888 | |
| x5 − 50x3 − 600x2 − 2000x − 11200 | |
| x5 + 110(5x3 + 20x2 − 360x + 800) | |
| x5 − 20x3 + 320x2 + 540x + 6368 | Reducible : -8 is a root |
| x5 − 20x3 − 160x2 − 420x − 8928 | Reducible : 8 is a root |
| x5 − 20x3 + 170x + 208 |
An infinite sequence of solvable quintics may be constructed, whose roots are sums of n-th roots of unity, with n = 10 k + 1 being a prime number:
| x5 + x4 − 4x3 − 3x2 + 3x + 1 | Roots:  |
| x5 + x4 − 12x3 − 21x2 + x + 5 | Root:  |
| y5 + y4 − 16y3 + 5y2 + 21y − 9 | Root:  |
| y5 + y4 − 24y3 − 17y2 + 41y − 13 | Root:  |
| y5 + y4 − 28y3 + 37y2 + 25y + 1 | Root: 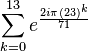 |
There are also two parameterized families of solvable quintics: The Kondo–Brumer quintic,
and the family depending on the parameters a,l,m
where
-
 Beyond radicals
Beyond radicals
Main article: Bring radical
If the Galois group of a quintic is not solvable, then the Abel-Ruffini theorem tells us that to obtain the roots it is necessary to go beyond the basic arithmetic operations and the extraction of radicals. About 1835,Jerrard demonstrated that quintics can be solved by using ultraradicals (also known as Bring radicals), the real roots of  for real numbers
for real numbers  . In 1858 Charles Hermite showed that the Bring radical could be characterized in terms of the Jacobi theta functions and their associated elliptic modular functions, using an approach similar to the more familiar approach of solving cubic equations by means oftrigonometric functions. At around the same time, Leopold Kronecker, using group theory developed a simpler way of deriving Hermite's result, as had Francesco Brioschi. Later, Felix Klein came up with a particularly elegant method that relates the symmetries of the icosahedron, Galois theory, and the elliptic modular functions that feature in Hermite's solution, giving an explanation for why they should appear at all, and develops his own solution in terms of generalized hypergeometric functions.[5] Similar phenomena occur in degree 7 (septic equations) and 11, as studied by Klein and discussed in icosahedral symmetry: related geometries.]
. In 1858 Charles Hermite showed that the Bring radical could be characterized in terms of the Jacobi theta functions and their associated elliptic modular functions, using an approach similar to the more familiar approach of solving cubic equations by means oftrigonometric functions. At around the same time, Leopold Kronecker, using group theory developed a simpler way of deriving Hermite's result, as had Francesco Brioschi. Later, Felix Klein came up with a particularly elegant method that relates the symmetries of the icosahedron, Galois theory, and the elliptic modular functions that feature in Hermite's solution, giving an explanation for why they should appear at all, and develops his own solution in terms of generalized hypergeometric functions.[5] Similar phenomena occur in degree 7 (septic equations) and 11, as studied by Klein and discussed in icosahedral symmetry: related geometries.]
 for real numbers
for real numbers  . In 1858 Charles Hermite showed that the Bring radical could be characterized in terms of the Jacobi theta functions and their associated elliptic modular functions, using an approach similar to the more familiar approach of solving cubic equations by means oftrigonometric functions. At around the same time, Leopold Kronecker, using group theory developed a simpler way of deriving Hermite's result, as had Francesco Brioschi. Later, Felix Klein came up with a particularly elegant method that relates the symmetries of the icosahedron, Galois theory, and the elliptic modular functions that feature in Hermite's solution, giving an explanation for why they should appear at all, and develops his own solution in terms of generalized hypergeometric functions.[5] Similar phenomena occur in degree 7 (septic equations) and 11, as studied by Klein and discussed in icosahedral symmetry: related geometries.]
. In 1858 Charles Hermite showed that the Bring radical could be characterized in terms of the Jacobi theta functions and their associated elliptic modular functions, using an approach similar to the more familiar approach of solving cubic equations by means oftrigonometric functions. At around the same time, Leopold Kronecker, using group theory developed a simpler way of deriving Hermite's result, as had Francesco Brioschi. Later, Felix Klein came up with a particularly elegant method that relates the symmetries of the icosahedron, Galois theory, and the elliptic modular functions that feature in Hermite's solution, giving an explanation for why they should appear at all, and develops his own solution in terms of generalized hypergeometric functions.[5] Similar phenomena occur in degree 7 (septic equations) and 11, as studied by Klein and discussed in icosahedral symmetry: related geometries.]
See also
References
| This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. Please help to improve this article by introducing more precise citations where appropriate. (March 2009) |
- ^ A. Cayley. On a new auxiliary equation in the theory of equation of the fifth order, Philosophical Transactions of the Royal Society of London (1861).
- ^ This formulation of Cayley's result is extracted from Lazard (2004) paper.
- ^ George Paxton Young. Solvable Quintics Equations with Commensurable Coefficients American Journal of Mathematics 10 (1888), 99–130 at JSTOR
- ^ http://www.math.harvard.edu/~elkies/trinomial.html
- ^ (Klein 1888); a modern exposition is given in (Tóth 2002, Section 1.6, Additional Topic: Klein's Theory of the Icosahedron, p. 66)
- Charles Hermite, "Sur la résolution de l'équation du cinquème degré",Œuvres de Charles Hermite, t.2, pp. 5–21, Gauthier-Villars, 1908.
- Felix Klein, Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree, trans. George Gavin Morrice, Trübner & Co., 1888. ISBN 0-486-49528-0.
- Leopold Kronecker, "Sur la résolution de l'equation du cinquième degré, extrait d'une lettre adressée à M. Hermite", Comptes Rendus de l'Académie des Sciences," t. XLVI, 1858 (1), pp. 1150–1152.
- Blair Spearman and Kenneth S. Williams, "Characterization of solvable quintics x5 + ax + b", American Mathematical Monthly, Vol. 101 (1994), pp. 986–992.
- Ian Stewart, Galois Theory 2nd Edition, Chapman and Hall, 1989. ISBN 0-412-34550-1. Discusses Galois Theory in general including a proof of insolvability of the general quintic.
- Jörg Bewersdorff, Galois theory for beginners: A historical perspective, American Mathematical Society, 2006. ISBN 0-8218-3817-2. Chapter 8 (The solution of equations of the fifth degree) gives a description of the solution of solvable quintics x5 + cx + d.
- Victor S. Adamchik and David J. Jeffrey, "Polynomial transformations of Tschirnhaus, Bring and Jerrard," ACM SIGSAM Bulletin, Vol. 37, No. 3, September 2003, pp. 90–94.
- Ehrenfried Walter von Tschirnhaus, "A method for removing all intermediate terms from a given equation," ACM SIGSAM Bulletin, Vol. 37, No. 1, March 2003, pp. 1–3.
- Daniel Lazard, "Solving quintics in radicals", in Olav Arnfinn Laudal, Ragni Piene, The Legacy of Niels Henrik Abel, pp. 207–225, Berlin, 2004,. ISBN 3-5404-3826-2. available at http://www.loria.fr/publications/2002/A02-R-449/A02-R-449.ps (broken link)
- Tóth, Gábor (2002), Finite Möbius groups, minimal immersions of spheres, and moduli
External links
- Calculator for solving Quintics
- Mathworld - Quintic Equation – more details on methods for solving Quintics.
- Solving the Quintic with Mathematica – poster on Quintic solutions
- [1] – Klein's book is available online
- Solving Solvable Quintics – a method for solving solvable quintics due to David S. Dummit.
- Polynomial Transformations of Tschirnhaus, Bring and Jerrard - a recent update of Tschirnhaus' paper by Victor S. Adamchik & David J. Jeffrey
- A method for removing all intermediate terms from a given equation - a recent English translation of Tschirnhaus' 1683 paper.
| ||||||||


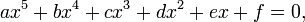
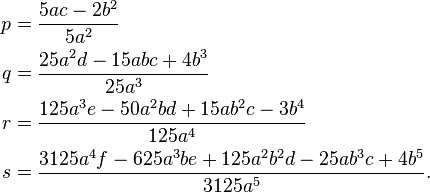

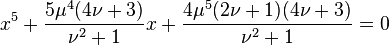





![x=1+\sqrt[5]{2}-\sqrt[5]{4}+\sqrt[5]{8}-\sqrt[5]{16}.](http://upload.wikimedia.org/math/8/0/2/8028fdefa5767d8e65d4d68297c33cc8.png)


![-(5^{2/5})x = \sqrt[5]{(a+c)^2(b-c)} + \sqrt[5]{(-a+c)(b-c)^2} + \sqrt[5]{(a+c)(b+c)^2} - \sqrt[5]{(-a+c)^2(b+c)}](http://upload.wikimedia.org/math/d/6/1/d61ff6f06c85e288577209a880b853f6.png)

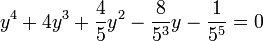


![x_k = \omega_k\sqrt[5]{y_1} + \omega_k^4\sqrt[5]{y_2}](http://upload.wikimedia.org/math/3/3/5/33552e35d77903c25732d0d433ed45b8.png)

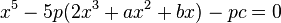
2 comments:
Yeah, interesting that the further members of a series of given kind are different in principle from the lower ones. It goes to show, we have right to logically assume continuation of previous attributes.
The single most important book to me in Popular Physics, is Peter Woit's Not Even Wrong. It's a tough read, no question, but um, so? Challenge yourself. Accept no substitutes.
Prior to reading Woit however, this book should be read. IMO.
Post a Comment