We'll take a break from the Physics Cycle here at MbI except to note that Supersymmetry, and therefore Superstring Theory, just got a bit of the old slap upside the head at the LHC, which you can read about here at RESONAANCES, here at Cosmic Variance, and here at Not Even Wrong.
Time to introduce a little Computer Science, an area in which I have next to zero expertise, but nevertheless find fascinating, and talk about something I had no knowledge of a week ago but which I find to be very cool:
The NAND logic gate, being the inverse of the well-known AND gate. In the Venn diagram above, you can see it includes everything exCEPT that which falls under AND.
From Wiki (various places):
The NAND gate is significant because any boolean function can be implemented by using a combination of NAND gates. This property is called functional completeness.
The Negated AND, NO AND or NAND gate is the opposite of the digital AND gate, and behaves in a manner that corresponds to the opposite of AND gate, as shown in the truth table below. A LOW output results only if both the inputs to the gate are HIGH. If one or both inputs are LOW, a HIGH output results.
Digital systems employing certain logic circuits take advantage of NAND's functional completeness. In complicated logical expressions, normally written in terms of other logic functions such as AND, OR, and NOT, writing these in terms of NAND saves on cost, because implementing such circuits using NAND gate yields a more compact result than the alternatives.
NAND gates can also be made with more than two inputs, yielding an output of LOW if all of the inputs are HIGH, and an output of HIGH if any of the inputs is LOW. These kinds of gates therefore operate as n-ary operators instead of a simple binary operator. Algebraically, these can be expressed as the function NAND(a, b, ..., n), which is logically equivalent to NOT(a AND b AND ... AND n).
Charles Sanders Peirce (1880) showed that NAND gates alone (or alternatively NOR gates alone) can be used to reproduce the functions of all the other logic gates, but his work on it was unpublished until 1935. The first published proof was by Henry M. Sheffer in 1913.
A logic gate is a physical model of a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Logic gates are primarily implemented electronically using diodes or transistors, but can also be constructed using electromagnetic relays (relay logic), fluidic logic, pneumatic logic, optics, molecules, or even mechanical elements.
With amplification, logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of Boolean logic, and therefore, all of the algorithms and mathematics that can be described with Boolean logic.
In the 1980s, schematics were the predominant method to design both circuit boards and custom ICs known as gate arrays. Today custom ICs and the field-programmable gate array are typically designed with Hardware Description Languages (HDL) such as Verilog or VHDL.
| Type | Distinctive shape | Rectangular shape | Boolean algebra between A & B | Truth table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | 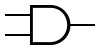 |  |  |
| ||||||||||||||||||
| OR |  | 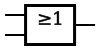 | A + B |
| ||||||||||||||||||
| NOT | 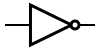 | 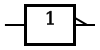 |  |
| ||||||||||||||||||
| In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble, and is used in logic diagrams to indicate a logical inversion between the external logic state and the internal logic state (1 to 0 or vice versa). On a circuit diagram it must be accompanied by a statement asserting that the positive logic convention or negative logic convention is being used (high voltage level = 1 or high voltage level = 0), respectively). The wedge is used in circuit diagrams to directly indicate an active-low (high voltage level = 0) input or output without requiring a uniform convention throughout the circuit diagram. This is called Direct Polarity Indication. See IEEE Std 91/91A and IEC 60617-12. Both the bubble and the wedge can be used on distinctive-shape and rectangular-shape symbols on circuit diagrams, depending on the logic convention used. On pure logic diagrams, only the bubble is meaningful. | ||||||||||||||||||||||
| NAND |  |  | 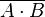 |
| ||||||||||||||||||
| NOR |  |  |  |
| ||||||||||||||||||
| XOR | 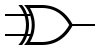 |  | 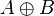 |
| ||||||||||||||||||
| XNOR | 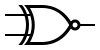 |  |  or or  |
| ||||||||||||||||||
Two more gates are the exclusive-OR or XOR function and its inverse, exclusive-NOR or XNOR. The two input Exclusive-OR is true only when the two input values are different, false if they are equal, regardless of the value. If there are more than two inputs, the gate generates a true at its output if the number of trues at its input is odd ([2]). In practice, these gates are built from combinations of simpler logic gates.
The NAND gate has the property of functional completeness. That is, any other logic function (AND, OR, etc.) can be implemented using only NAND gates. An entire processor can be created using NAND gates alone. In TTL ICs using multiple-emitter transistors, it also requires fewer transistors than any other gate.






4 comments:
Your website is very beautiful or Articles. I love it thank you for sharing for everyone. Mountain View Private School
Hiya mate, great writeup! I make youtube vids on comp science. I wanted to do one on nand gates and love the title of this blog! I was wondering if you’d mind if I use the name? Happy to credit you and link to this blog in the video description. Please let me know. Thanks, Chris.
It was fantastic. Basic logic gates with truth table are also required. Truth tables are looking difficult in arrangements.
Post a Comment