What a tragedy. In this animation someone travels through a wormhole, from the University of Tübingen in southwest Germany to the French seacoast in Boulogne-sur-Mer.
Click Here and download the long animation to see the wormhole journey.
Where is the tragedy you say? He is going to the beach!
Oh yes, the beach. That is the good part. The terrible part is that he spends very little time there, and then, RETURNS back to University, almost right away!
Beach? School? Beach? Work? Beach? Anywhere else? Beach? Hmmmmm.
This is a tough question, yes? NO !!! ALways choose the beach, over everything else!
Well perhaps he forgot his towel, and it will be a happy ending after all.. :-)
WORMHOLE MATHEMATICS - Quickie version
Theories of wormhole metrics describe the spacetime geometry of a wormhole and serve as theoretical models for time travel. An example of a (traversable) wormhole metric is the following:
Click here for the Wikipedia article on Wormholes. Then, go to the beach!
 |
| Beach = Good |
 |
| School/Work = Eh. Not as good as Beach! |

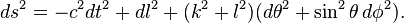
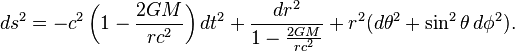
4 comments:
I'm not quite aware of how I should interpret these equations so as to understand why one can travel so quickly trough space-time with wormholes.
Dear Pr. Colyer, can you explain this to me?
Sure, however, unless you can find a bunch of exotic matter, create some negative energy, and figure out a way to channel infinite energy, you can relax and not worry about creating a wormhole anytime soon. :-)
That's the quick answer.
Actually, it's been a while since I studied this, but you can relax the Infinite energy condition. But you'll need IE though to travel faster than light, thanks to the Alciberre drive which fakes nature into thinking Inertia doesn't exist around your starship. So we don't have to worry about ever doing that, either.
All these things: wormholes, time travel, and FTL are possible thanks to Einstein's General Relativity equations. Theoretically. Practically? No. The Wiki article and links do a good job of explaining why not. Kip Thorne has written books about the subject where yes, he admits also, these things are impractical.
But it's fun to dream and think we will have them some day. :-)
Dear Sirs
Do whormholes exist?
They are possible for the solutions of the space-time metric kinematical differential equation of Minkowski space-time, the mathematics of these are not so difficult as the partial differential equations of general relativity, as the space time metric of minskowski is an ordinary quadratic differential equation, learnable in the first years of mathematics os astronomy faculty, but ho wis time and matter on them, they should be defined in mathematical manouvers of tensor calculus, but do they apply to reality, can we travel on them without being destroyed, do they exist in flat perturbed space? are they perturbed by gravitation? won't one die instanly trought them? sometimes mathematics is too manouverable, and one has to trust racionality to act. Please consult the works os Francico S. N. Lobo in "search" www.clix.pt
Paul Rose/M. Lapa
Very significant Information for us, I have think the representation of this Information is actually superb one. This is my first visit to your site. Chicwish
Post a Comment