The realm of the very large, of galaxies and the filaments of same and the voids between them have always fascinated me.
Perhaps chief among them are the jets, called polar jets when non-relativistic and relativistic when not, that shoot out from the poles of everything from neutron stars to stellar-sized black holes to galactic-sized black holes to quasars (active galaxies).
Apparently there are 2 competing theories on the origin and mechanism of the faster relativistic ones, that I just became aware of. I'm curious if anyone knows how things are progressing to solving this interesting mystery, given the fantastic amount of new data the observatories on earth and in space are providing.
These are also drawn into the mathematics of "Frame-dragging", an interesting field in its own right, which basically says that matter in a rotating body drags space-time due to the rotation, which was predicted in 1918 based on Einstein's field equations of General Relativity.
The Mathematics of General Relativity are pretty straight forward assuming one has taken the first four college courses in Calculus, which end with the extremely important PDE (Partial Differential Equations) in 4th-semester Calc IV.
Frame-dragging is an excellent application of same. From two different Wiki articles:
Relativistic jets are extremely powerful jets of plasma which emerge from presumed massive objects at the centers of some active galaxies, notably radio galaxies and quasars. Their lengths can reach several thousand[1] or even hundreds of thousands of light years.[2] The hypothesis is that the twisting of magnetic fields in the accretion disk collimates the outflow along the rotation axis of the central object, so that when conditions are suitable, a jet will emerge from each face of the accretion disk. If the jet is oriented along the line of sight to Earth, relativistic beaming will change its apparent brightness. The mechanics behind both the creation of the jets[3][4] and the composition of the jets[5] are still a matter of much debate in the scientific community; it is hypothesized that the jets are composed of an electrically neutral mixture of electrons, positrons, and protons in some proportion.

Elliptical Galaxy M87 emitting a relativistic jet, as seen by Hubble Space Telescope's WFPC2 in the visible spectrum.
The general hypothesis among astrophysicists is that the formation of relativistic jets is the key to explaining the production of gamma-ray bursts. These jets have Lorentz factors of ~100 (that is, speeds of roughly 0.99995c), making them one of the swiftest celestial objects currently known.
Rotating black hole as energy source
Because of the enormous amount of energy needed to launch a relativistic jet, some jets are thought to be powered by spinning black holes. There are two competing theories for how the energy is transferred from the black hole to the jet.- Blandford-Znajek process.[6] This is the most popular theory for the extraction of energy from the central black hole. The magnetic fields around the accretion disk are dragged by the spin of the black hole. The relativistic material is possibly launched by the tightening of the field lines.
- Penrose mechanism.[7] This extracts energy from a rotating black hole by frame dragging. This theory was later proven to be able to extract relativistic particle energy and momentum,[8] and subsequently shown to be a possible mechanism for the formation of jets.[9]
Albert Einstein's theory of general relativity predicts that rotating bodies drag spacetime around themselves in a phenomenon referred to as frame-dragging. The rotational frame-dragging effect was first derived from the theory of general relativity in 1918 by the Austrian physicists Josef Lense and Hans Thirring, and is also known as the Lense–Thirring effect.[1][2][3] Lense and Thirring predicted that the rotation of an object would alter space and time, dragging a nearby object out of position compared with the predictions of Newtonian physics. The predicted effect is small—about one part in a few trillion. To detect it, it is necessary to examine a very massive object, or build an instrument that is very sensitive. More generally, the subject of field effects caused by moving matter is known as gravitomagnetism.
Frame dragging effects
Rotational frame-dragging (the Lense–Thirring effect) appears in the general principle of relativity and similar theories in the vicinity of rotating massive objects. Under the Lense–Thirring effect, the frame of reference in which a clock ticks the fastest is one which is rotating around the object as viewed by a distant observer. This also means that light traveling in the direction of rotation of the object will move around the object faster than light moving against the rotation as seen by a distant observer. It is now the best-known effect, partly thanks to the Gravity Probe B experiment.Linear frame dragging is the similarly inevitable result of the general principle of relativity, applied to linear momentum. Although it arguably has equal theoretical legitimacy to the "rotational" effect, the difficulty of obtaining an experimental verification of the effect means that it receives much less discussion and is often omitted from articles on frame-dragging (but see Einstein, 1921).[4]
Static mass increase is a third effect noted by Einstein in the same paper.[5] The effect is an increase in inertia of a body when other masses are placed nearby. While not strictly a frame dragging effect (the term frame dragging is not used by Einstein), it is demonstrated by Einstein to derive from the same equation of general relativity. It is also a tiny effect that is difficult to confirm experimentally.
Experimental tests of frame-dragging
In 1976 Van Patten and Everitt[6][7] proposed to implement a dedicated mission aimed to measure the Lense–Thirring node precession of a pair of counter-orbiting spacecraft to be placed in terrestrial polar orbits with drag-free apparatus. A somewhat equivalent, cheaper version of such an idea was put forth in 1986 by Ciufolini[8] who proposed to launch a passive, geodetic satellite in an orbit identical to that of the LAGEOS satellite, launched in 1976, apart from the orbital planes which should have been displaced by 180 deg apart: the so-called butterfly configuration. The measurable quantity was, in this case, the sum of the nodes of LAGEOS and of the new spacecraft, later named LAGEOS III, LARES, WEBER-SAT. Although extensively studied by various groups,[9][10] such an idea has not yet been implemented. The butterfly configuration would allow, in principle, to measure not only the sum of the nodes but also the difference of the perigees,[11][12][13] although such Keplerian orbital elements are more affected by the non-gravitational perturbations like the direct solar radiation pressure: the use of the active, drag-free technology would be required. Other proposed approaches involved the use of a single satellite to be placed in near polar orbit of low altitude,[14][15] but such a strategy has been shown to be unfeasible.[16][17][18] In order to enhance the possibilities of being implemented, it has been recently claimed that LARES/WEBER-SAT would be able to measure the effects[19] induced by the multidimensional braneworld model by Dvali, Gabadaze and Porrati[20] and to improve by two orders of magnitude the present-day level of accuracy of the equivalence principle.[21] Such claims have been shown to be highly unrealistic.[22][23]Limiting the scope to the scenarios involving existing orbiting bodies, the first proposal to use the LAGEOS satellite and the Satellite Laser Ranging (SLR) technique to measure the Lense–Thirring effect dates back to 1977–1978.[24][25] Tests have started to be effectively performed by using the LAGEOS and LAGEOS II satellites in 1996,[26] according to a strategy[27] involving the use of a suitable combination of the nodes of both satellites and the perigee of LAGEOS II. The latest tests with the LAGEOS satellites have been performed in 2004-2006[28][29] by discarding the perigee of LAGEOS II and using a linear combination[30][31][32][33][34][35] involving only the nodes of both the spacecraft. Although the predictions of general relativity are compatible with the experimental results, the realistic evaluation of the total error raised a debate.[36][37][38][39][40][41] Another test of the Lense–Thirring effect in the gravitational field of Mars, performed by suitably interpreting the data of the Mars Global Surveyor (MGS) spacecraft, has been recently reported.[42] There is also debate about this test.[43][44][45] Attempts to detect the Lense–Thirring effect induced by the Sun's rotation on the orbits of the inner planets of the Solar System have been reported as well:[46] the predictions of general relativity are compatible with the estimated corrections to the perihelia precessions,[47] although the errors are still large. However, the inclusion of the radiometric data from the Magellan orbiter recently allowed Pitjeva to greatly improve the determination of the unmodelled precession of the perihelion of Venus. It amounts to −0.0004 ± 0.0001 arcseconds/century, while the Lense–Thirring effect for the Venus' perihelion is just -0.0003 arcseconds/century.[48] The system of the Galilean satellites of Jupiter was investigated as well,[49] following the original suggestion by Lense and Thirring.
The Gravity Probe B experiment[50][51] is currently under way to experimentally measure another gravitomagnetic effect, i.e. the Schiff precession of a gyroscope,[52][53] to an expected 1% accuracy or better. Unfortunately, it seems that such an ambitious goal will not be achieved: indeed, first preliminary results released in April 2007 point toward a so far obtained accuracy of[54] 256–128%, with the hope of reaching about 13% in December 2007.[55] However, in 2008 the Senior Review Report of the NASA Astrophysics Division Operating Missions stated that it is unlikely that Gravity Probe B team will be able to reduce the errors to the level necessary to produce a convincing test of currently-untested aspects of General Relativity (including Frame-dragging).[56][57]
A 1% measurement of the Lense–Thirring effect in the gravitational field of the Earth could be obtained by launching at least two entirely new satellites, preferably with active mechanisms of compensation of the non-gravitational forces, in eccentric orbits, as stated in 2005 by Lorenzo Iorio.[58] Recently, the Italian Space Agency (ASI) has announced that the LARES satellite should be launched with a Vega rocket at the beginning of 2011.[59] The goal of LARES is to measure the Lense–Thirring effect to 1%, but there are doubts that this can be achieved,[60][61][62][63][64] mainly due to the relatively low-orbit which LARES should be inserted into bringing into play more mismodelled even zonal harmonics.[clarification needed] That is, spherical harmonics of the Earth's gravitational field caused by mass concentrations (like mountains) can drag a satellite in a way which may be difficult to distinguish from frame-dragging. Recently, an indirect test of the gravitomagnetic interaction accurate to 0.1% has been reported by Murphy et al. with the Lunar laser ranging (LLR) technique,[65] but Kopeikin questioned the ability of LLR to be sensitive to gravitomagnetism.[66]
In the case of stars orbiting close to a spinning, supermassive black hole, frame dragging should cause the star's orbital plane to precess about the black hole spin axis. This effect should be detectable within the next few years via astrometric monitoring of stars at the center of the Milky Way galaxy.[67] By comparing the rate of orbital precession of two stars on different orbits, it is possible in principle to test the no-hair theorems of general relativity, in addition to measuring the spin of the black hole.[68]
Astronomical evidence

Relativistic Jet. The environment around the AGN where the relativistic plasma is collimated into jets which escape along the pole of the supermassive black hole
Mathematical derivation of frame-dragging
Frame-dragging may be illustrated most readily using the Kerr metric,[72][73] which describes the geometry of spacetime in the vicinity of a mass M rotating with angular momentum J
The two surfaces on which the Kerr metric appears to have singularities; the inner surface is the spherical event horizon, whereas the outer surface is an oblate spheroid. The ergosphere lies between these two surfaces; within this volume, the purely temporal component gtt is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character.
Lense–Thirring effect inside a rotating shell
Inside a rotating spherical shell the acceleration due to the Lense–Thirring effect would be [75]See also
External links
- NASA RELEASE: 04-351 As The World Turns, It Drags Space And Time
- New Scientist press release of the MGS test by Iorio in the gravitational field of Mars
- Paper by Giampiero Sindoni, Claudio Paris and Paolo Ialongo about the Mars-MGS test (unpublished)
- Paper by G. Felici about the Mars-MGS test (unpublished)
- Paper by Kris Krogh about the Mars-MGS test
- Reply by Ignazio Ciufolini and Erricos Pavlis about some criticisms by Iorio
- Frame dragging applied to relativistic jets
- Frame Dragging
- Duke University press release: General Relativistic Frame Dragging
- MSNBC report on X-ray observations
- Ciufolini et al. LAGEOS paper 1997 - 25% error
- Ciufolini update Sep 2002 - 20% error
- Press release regarding LAGEOS study
- Preprint by Ries et al.
- Ciufolini and Pavlis Nature new article on 2004 re-analysis of the LAGEOS data
- Iorio New Astronomy general paper with full references
- Iorio J. of Geodesy paper on the impact of the secular variations of the even zonal harmonics of the geopotential
- Iorio Planetary Space Science paper
- Iorio General Relativity and Gravitation paper on LARES
- Iorio Advances in Space Research paper on LARES
- An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense–Thirring Effect with Satellite Laser Ranging IorioSpace Science Reviews paper on LARES
- Advances in the measurement of the Lense–Thirring effect with Satellite Laser Ranging in the gravitational field of the Earth Iorio invited book chapter on LARES
Categories: Tests of general relativity | Effects of gravitation | Frames of reference | Fundamental physics concepts


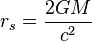




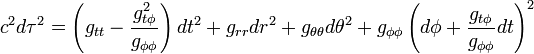
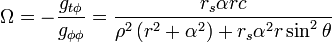



![\bar{a} = -2d_1 \left( \bar{ \omega} \times \bar v \right) - d_2 \left[ \bar{ \omega} \times \left( \bar{ \omega} \times \bar{r} \right) + 2\left( \bar{ \omega}\bar{r} \right) \bar{ \omega} \right]](http://upload.wikimedia.org/math/9/8/c/98c371696910069c25f914790a842201.png)
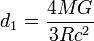

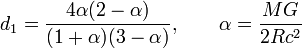
1 comment:
I believe there is no frame-dragging effect of gravity on mass, only on electromagnetic energy!
Curiously, the Lense-Thirring effect in Gravity Probe B has the same value than the geodetic effect of the Earth around the Sun.
NASA error?
An interesting experiment!
Understanding Gravity Probe-B experiment without math
http://www.molwick.com/en/gravitation/082-gravity-probe-b.html
http://www.molwick.com/en/gravitation/r-lense-thirring-frame-dragging.jpg
Post a Comment