How about cubes? Yes that will do it, Cubes "tessellate", that is to say "fill" space, with no gaps. Spheres certainly don't. A cube is one of the five Regular polyhedrons that so fascinated the ancients, along with the tetrahedron, the octahedron, the dodecahedron, and the icosahedron.
I once made Archimedes' mistake, which is that tetrahedrons fill space too. But they don't. However, a combination of tetrahedrons and octahedron do, which I figured out for myself, only to find out through further research that so had many others, long ago.
So, hy did Archimedes and I make this mistake? Possibly because of the octa- and tetra- thing, and possibly because triangles tessellate well in 2-space.
So the cube (aka the hexahedron), is the only one of the 5 regular polyhedra to fill space. Anything else?
Yes, the Johnson solid known as gyrobifastgium, pictured above.
Anything else?
Yes, several more things: hexagonal, square and triangular prisms, and the Archimedean solid known as the Truncated octahedron
As so:
The truncated octahedron exists in three different convex uniform honeycombs (space-filling tessellations):
| Bitruncated cubic | Cantitruncated cubic | Truncated alternated cubic |
|---|---|---|
 |  | 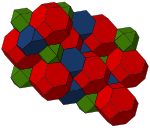 |
Bitruncated cubic:
This honeycomb has three uniform constructions, with the truncated octahedral cells having different Coxeter groups and Wythoff constructions:
- C~3 or [4,3,4] group - Two types of truncated octahedra in 1:1 ratio. Half from the original cells of a cubic honeycomb, and half are centered on the vertices of the original honeycomb.
- B~3 or [4,31,1] group - Three types of truncated octahedra in 2:1:1 ratios.
- A~3 or [3[4]] group - Four types of truncated octahedra in 1:1:1:1 ratios.
 A 2-colored honeycomb with C~3 symmetry. |  A 3-colored honeycomb with B~3 symmetry. |  A 4-colored honeycomb with A~3 symmetry. |
Here is the net:
And in fact, there are many more, such as this:
 | ||
| Rhombic dodecahedron |
and
 | ||||
| Rhombo-hexagonal dodecahedron |



No comments:
Post a Comment