Multiplication by Infinity: Torricelli's Trumpet

Monday, April 4, 2011

Torricelli's Trumpet

Gabriel's Horn (also called Torricelli's trumpet) is a geometric figure which has infinite surface area but encloses a finite volume. The name refers to the tradition identifying the Archangel Gabriel as the angel who blows the horn to announce Judgment Day, associating the divine, or infinite, with the finite. The properties of this figure were first studied by Italian physicist and mathematician Evangelista Torricelli.

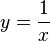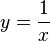Gabriel's horn is formed by taking the graph of $y= \frac{1} {x}$ , with the domain $x \ge 1$ (thus avoiding the asymptote at x = 0) and rotating it in three dimensions about the x-axis. The discovery was made using Cavalieri's principle before the invention of calculus, but today calculus can be used to calculate the volume and surface area of the horn between x = 1 and x = a, where a > 1. Using integration (see Solid of revolution and Surface of revolution for details), it is possible to find the volume

V

and the surface area

A

$V = \pi \int_{1}^{a} {1 \over x^2}\mathrm{d}x = \pi \left( 1 - {1 \over a} \right)$

$A = 2\pi \int_1^a \frac{\sqrt{1 + \frac{1}{x^4}}}{x}\mathrm{d}x > 2\pi \int_1^a \frac{\sqrt{1}}{x}\ \mathrm{d}x = 2\pi \ln a.$

a

can be as large as required, but it can be seen from the equation that the volume of the part of the horn between

x = 1

and

x = a

will never exceed

π

; however, it will get closer and closer to $π$ as

a

becomes larger. Mathematically, the volume approaches

π

as $a$ approaches infinity. Using the limit notation of calculus, the volume may be expressed as:

$\lim_{a \to \infty}\pi \left( 1 - {1 \over a} \right) = \pi.$

This is so because as

a

approaches infinity,

1 / a

approaches zero. This means the volume is

π

(1 - 0) which equals

π

As for the area, the above shows that the area is greater than

2π

times the natural logarithm of

a

. There is no upper bound for the natural logarithm of

a

as it approaches infinity. That means, in this case, that the horn has an infinite surface area. That is to say;

$2 \pi \ln a \rightarrow \infty$ as $a \rightarrow \infty$

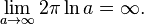
$\lim_{a \to \infty}2 \pi \ln a = \infty.$

Apparent paradox

When the properties of Gabriel's Horn were discovered, the fact that the rotation of an infinite curve about the x-axis generates an object of finite volume was considered paradoxical. However the explanation is that the bounding curve, $y= \tfrac{1}{x}$ , is simply a special case–just like the simple harmonic series (Σ1/x¹)–for which the successive area 'segments' do not decrease rapidly enough to allow for convergence to a limit. For volume segments (Σ1/x²) however, and in fact for any generally constructed higher degree curve (eg y = 1/x^1.001), the same is not true and the rate of decrease in the associated series is sufficiently rapid for convergence to a (finite) limiting sum.

Christiaan Huygens and François Walther de Sluze found a surface of revolution with related properties: an infinitely high solid with finite volume (so it can be made of finite material) which encloses an infinitely large cavity. This was obtained by rotating the non-negative part defined on 0≤x<1 of the cissoid of Diocles $y^2=\tfrac{x^3}{1-x}$ around the y-axis. De Sluze described it as a "drinking vessel that has small weight but that even the hardiest drinker could not empty".

Together these two paradoxes formed part of a great dispute over the nature of infinity involving many of the key thinkers of the time including Thomas Hobbes, John Wallis and Galileo.^[1]