The Largest Possible Ordered Field

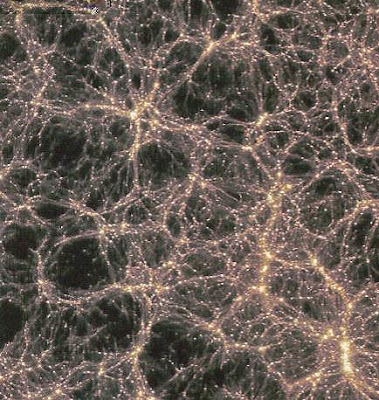
Neurons? Or Galactic Filaments/Voids?

In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller inabsolute value than any positive real number. The surreals share many properties with the reals, including a total order ≤ and the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they form an ordered field.^[1] In a rigorous set theoretic sense, the surreal numbers are the largest possible ordered field; all other ordered fields, such as the rationals, the reals, the rational functions, the Levi-Civita field, the superreal numbers, and the hyperreal numbers, are subfields of the surreals. The surreals also contain alltransfinite ordinal numbers reachable in the set theory in which they are constructed.

The definition and construction of the surreals is due to John Horton Conway. They were introduced in Donald Knuth's 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. This book is a mathematical novelette, and is notable as one of the rare cases where a new mathematical idea was first presented in a work of fiction. In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had simply called numbers originally. Conway liked the new name, and later adopted it himself. Conway then described the surreal numbers and used them for analyzing games in his 1976 book On Numbers and Games.

Contents  [hide] 1 Construction 1.1 Forms 1.2 Numeric forms 1.3 Equivalence classes of numeric forms 1.4 Order 1.5 Induction 2 Arithmetic 2.1 Negation 2.2 Addition 2.3 Multiplication 2.4 Consistency 2.5 Arithmetic closure 3 "To Infinity ..." 3.1 Contents of Sω 4 "... and Beyond." 5 Powers of ω 6 Games 7 Application to combinatorial game theory 8 Alternative realization 8.1 Sign expansion 8.1.1 Definitions 8.1.2 Addition and multiplication 8.1.3 Correspondence with Conway 8.2 Axiomatic approach 9 See also 10 Notes 11 Further reading 12 External links

The Wikipedia Page is too long to publish. Click on any Table of Contents item above to read it.

Personally, I find the study of Infinitesimals interesting, with possible applications to Physics.

Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.

In common speech, an infinitesimal object is an object which is smaller than any feasible measurement, but not zero in size; or, so small that it cannot be distinguished from zero by any available means. Hence, when used as an adjective, "infinitesimal" in the vernacular means "extremely small".

Archimedes exploited infinitesimals in The Method to find areas of regions and volumes of solids. The classical authors tended to seek to replace infinitesimal arguments by arguments by exhaustion which they felt were more reliable. The 15th century saw the pioneering work of Nicholas of Cusa, further developed in the 17th century by Johannes Kepler, in particular calculation of area of a circle by representing the latter as an infinite-sided polygon. Simon Stevin developed a continuum of decimals in the 16th century. Bonaventura Cavalieri's method of indivisibles led to an extension of the results of the classical authors. The method of indivisibles related to geometrical figures as being composed of entities of codimension 1. John Wallis's infinitesimals differed from indivisibles in that he would decompose geometrical figures into infinitely thin building blocks of the same dimension as the figure, preparing the ground for general methods of the integral calculus. 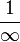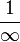He exploited an infinitesimal denoted  in area calculations.

Pierre de Fermat, inspired by Diophantus, introduced the concept adequality, i.e. "adequate" or approximate equality (up to an infinitesimal error), which ultimately played a key role in a modern mathematical implementation of infinitesimal definitions of derivative and integral. The use of infinitesimals in Leibniz relied upon a heuristic principle called the Law of Continuity: what succeeds for the finite numbers succeeds also for the infinite numbers and vice versa. The 18th century saw routine use of infinitesimals by such greats as Leonhard Euler andJoseph Lagrange. Augustin-Louis Cauchy exploited infinitesimals in defining continuity and an early form of a Dirac delta function. As Cantor and Dedekind were developing more abstact versions of Stevin's continuum, Paul du Bois-Reymond wrote a series of papers on infinitesimal-enriched continua based on growth rates of functions. Du Bois-Reymond's work inspired both Emile Borel and Thoralf Skolem. Skolem developed the first non-standard models of arithmetic in 1934. A mathematical implementation of both the law of continuity and infinitesimals was achieved by Abraham Robinson in 1961, who developed non-standard analysis based on earlier work by Edwin Hewitt in 1948 and Jerzy Łoś in 1955. The hyperrealsimplement an infinitesimal-enriched continuum and the transfer principle implements Leibniz's law of continuity.

Contents  [hide] 1 History of the infinitesimal 2 First-order properties 3 Number systems that include infinitesimals 3.1 Formal series 3.1.1 Laurent series 3.1.2 The Levi-Civita field 3.1.3 Transseries 3.2 Surreal numbers 3.3 The hyperreal system 3.4 Superreals 3.5 Smooth infinitesimal analysis 4 Infinitesimal delta functions 5 Logical properties 6 See also 7 Notes 8 References