Thanks much to Pat Ballew of Pat's Blog for the following fascinating and cool video:
In physics, a moiré pattern (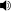 /mwɑːˈreɪ/; French: [mwaʁe]) is an interference pattern created, for example, when two grids are overlaid at an angle, or when they have slightly different mesh sizes.
/mwɑːˈreɪ/; French: [mwaʁe]) is an interference pattern created, for example, when two grids are overlaid at an angle, or when they have slightly different mesh sizes.
Contents[hide] |
Etymology
The term originates from moire (or moiré in its French form), a type of textile, traditionally of silk but now also of cotton or synthetic fiber, with a rippled or 'watered' appearance.
The history of the word moiré is complicated. The earliest agreed origin is the Arabic mukhayyar (مُخَيَّر in Arabic, which means chosen), a cloth made from the wool of the Angora goat, from khayyara (خيّر in Arabic), 'he chose' (hence 'a choice, or excellent, cloth'). It has also been suggested that the Arabic word was formed from the Latin marmoreus, meaning 'like marble'. By 1570 the word had found its way into English as mohair. This was then adopted into French as mouaire, and by 1660 (in the writings of Samuel Pepys) it had been adopted back into English as moire or moyre. Meanwhile the French mouaire had mutated into a verb, moirer, meaning 'to produce a watered textile by weaving or pressing', which by 1823 had spawned the adjective moiré. Moire (pronounced "mwar") and moiré (pronounced "mwar-ay") are now used somewhat interchangeably in English, though moire is more often used for the cloth and moiré for the pattern.
Pattern formation
Moiré patterns are often an undesired artifact of images produced by various digital imaging and computer graphics techniques, for example whenscanning a halftone picture or ray tracing a checkered plane (the latter being a special case of aliasing, due to undersampling a fine regular pattern).[1] This can be overcome in texture mapping through the use of mipmapping and anisotropic filtering
The drawing on the upper right shows a moiré pattern. The lines could represent fibers in moiré silk, or lines drawn on paper or on a computer screen. The nonlinear interaction of the optical patterns of lines creates a real and visible pattern of roughly parallel dark and light bands, the moiré pattern, superimposed on the lines.[2]
More complex line moiré patterns are created if the lines are curved or not exactly parallel. Moiré patterns revealing complex shapes, or sequences of symbols embedded in one of the layers (in form of periodically repeated compressed shapes) are created with shape moiré, otherwise called band moiré patterns. One of the most important properties of shape moiré is its ability to magnify tiny shapes along either one or both axes, that is, stretching. A common 2D example of moiré magnification occurs when viewing a chain-link fence through a second chain-link fence of identical design. The fine structure of the design is visible even at great distances.
Implications in printing full-color images
In graphic arts and prepress, the usual technology for printing full-color images involves the superimposition of halftone screens. These are regular rectangular dot patterns—often four of them, printed in cyan, yellow, magenta, and black. Some kind of moiré pattern is inevitable, but in favorable circumstances the pattern is "tight;" that is, the spatial frequency of the moiré is so high that it is not noticeable. In the graphic arts, the term moirémeans an excessively visible moiré pattern. Part of the prepress art consists of selecting screen angles and halftone frequencies which minimize moiré. The visibility of moiré is not entirely predictable. The same set of screens may produce good results with some images, but visible moiré with others.
In manufacturing industries, these patterns are used for studying microscopic strain in materials: by deforming a grid with respect to a reference grid and measuring the moiré pattern, the stress levels and patterns can be deduced. This technique is attractive because the scale of the moiré pattern is much larger than the deflection that causes it, making measurement easier.
Moirés on TV screens
Moiré patterns are commonly seen on television screens directly when a person is wearing a shirt or jacket of a particular weave or pattern, such as a houndstooth jacket, due to sampling problems in the television camera. As the person moves about, the Moiré pattern is quite noticeable. Because of this, newscasters and other professionals who appear on TV regularly are instructed to avoid clothing which could cause the effect, more commonly known as 'strobing'.
Photographs of a TV screen taken with a digital camera often exhibit moiré patterns.
The Moiré effect is used in shoreside beacons to mark underwater hazards (usually pipelines or cables).[3] The Moiré effect creates arrows that 'point' towards an imaginary line marking the hazard. As you pass over the hazard, the arrows on the beacon appear to become vertical bands before 'changing' back to arrows pointing in the reverse direction. An example can be found in the UK on the East shore of Southampton water, opposite Fawley oil refinery (50°51′21.63″N 1°19′44.77″W). Similar Moiré effect beacons can be used to guide mariners to the centre point of an oncoming bridge (here you would position the vessel so that you could see vertical lines - denoting the 'centreline').
[edit]Calculations
[edit]Moiré of parallel patterns
[edit]Geometrical approach
Let us consider two patterns made of parallel and equidistant lines, e.g., vertical lines. The step of the first pattern is p, the step of the second is p+δp, with 0<δ<1.
If the lines of the patterns are superimposed at the left of the figure, the shift between the lines increase when going to the right. After a given number of lines, the patterns are opposed: the lines of the second pattern are between the lines of the first pattern. If we look from a far distance, we have the feeling of pale zones when the lines are superimposed, (there is white between the lines), and of dark zones when the lines are "opposed".
The middle of the first dark zone is when the shift is equal to p/2. The nth line of the second pattern is shifted by n·δp compared to the nthline of the first network. The middle of the first dark zone thus corresponds to
- n·δp = p/2
that is
 .
.
The distance d between the middle of a pale zone and a dark zone is
the distance between the middle of two dark zones, which is also the distance between two pale zones, is
From this formula, we can see that :
- the bigger the step, the bigger the distance between the pale and dark zones;
- the bigger the discrepancy δp, the closer the dark and pale zones; a great spacing between dark and pale zones mean that the patterns have very close steps.
Of course, when δp = p/2, we have a uniformly grey figure, with no contrast.
The principle of the moiré is similar to the Vernier scale.
Interferometric approach
Let us consider now two transparent patterns with a contrast I that varies with a sinusoidal law:
(the steps are respectively p1 = 1/k1 and p2 = 1/k2), when the patterns are superimposed, the resulting intensity (interference) is
with the Euler's formula:
We can see that the resulting intensity is made of a sinus law with a high "spatial frequency" (wave number) which is the average of the spatial frequencies of the two patterns, and of a sinus law with a low spatial frequency which is the half of the difference between the spatial frequencies of the two patterns. This second component is an "envelope" for the first sinus law. The wavelength λ of this component is the inverse of the spatial frequency
if we consider that's p1 = p and p2 = p+δp:
 .
.
The distance between the zeros of this envelope is λ/2, and the maxima of amplitude are also spaced by λ/2; we thus obtain the same results as the geometrical approach, with a discrepancy of p/2 which is the uncertainty linked to the reference that is considered: pattern 1 or pattern 2. This discrepancy is negligible when δp << p.
This phenomenon is similar to the stroboscopy.
Rotated patterns
Let us consider two patterns with the same step p, but the second pattern is turned by an angle α. Seen from far, we can also see dark and pale lines: the pale lines correspond to the lines of nodes, that is, lines passing through the intersections of the two patterns.
If we consider a cell of the "net", we can see that the cell is a rhombus: it is a parallelogram with the four sides equal to d = p/sin α; (we have a righttriangle which hypothenuse is d and the side opposed to the α angle is p).
The pale lines correspond to the small diagonal of the rhombus. As the diagonals are the bisectors of the neighbouring sides, we can see that the pale line makes an angle equal to α/2 with the perpendicular of the lines of each pattern.
Additionally, the spacing between two pale lines is D, the half of the big diagonal. The big diagonal 2D is the hypothenuse of a right triangle and the sides of the right angle are d(1+cos α) and p. The Pythagorean theorem gives:
- (2D)2 : d2(1+cos α)2 + p2
id est
thus
When α is very small (α < π/6), the following approximations can be done:
- sin α ≈ α
- cos α ≈ 1
thus
- D ≈ p / α
α is of course in radian.
We can see that the smaller the α, the farthest the pale lines; when the both patterns are parallel (α = 0), the spacing between the pale lines is "infinite" (there is no pale line).
There are thus two ways to determine α: by the orientation of the pale lines and by their spacing
- α ≈ p / D
If we choose to measure the angle, the final error is proportional to the measurement error. If we choose to measure the spacing, the final error is proportional to the inverse of the spacing. Thus, for the small angles, it is best to measure the spacing.
Application to strain measurement
The moiré effect can be used in strain measurement: the operator just has to draw a pattern on the object, and superimpose the reference pattern to thedeformed pattern on the deformed object.
A similar effect can be obtained by the superposition of an holographic image of the object to the object itself: the hologram is the reference step, and the difference with the object are the deformations, which appear as pale and dark lines.
Application to image processing
Some image scanner driver programs provide an optional filter, called a "descreen" filter, to remove Moiré-pattern artifacts which would otherwise be produced when scanning printed halftone images to produce digital images.[4]
See also
References
- ^ Moire in scanning, scantips.com, accessed July 2009
- ^ Anil K. Jain, Mário Figueiredo, and Josiane Zerubia (editors) (2001). Energy Minimization Methods in Computer Vision and Pattern Recognition. Springer.
- ^ http://www.online-list-of-lights.info/html/enleuchtfeuer.html
- ^ Scanning Images in magazines/books/newspapers at scantips.com; visited 22 April 2010.
External links
A series of oil paintings based on Moiré principles by British artist, Pip Dickens
- A live demonstration of the Moiré effect that stems from interferences between circles
- An interactive example of various Moiré patterns Use arrow keys and mouse to manipulate layers.




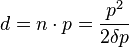
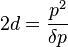

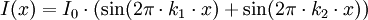
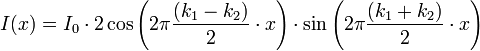




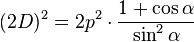



No comments:
Post a Comment