Simple harmonic motion refers to the periodic sinusoidal oscillation of an object or quantity. Simple harmonic motion is executed by any quantity obeying the differential equation
(1) |
where  denotes the second derivative of
denotes the second derivative of  with respect to
with respect to 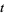 , and
, and 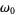 is the angular frequency of oscillation. This ordinary differential equation has an irregular singularity at
is the angular frequency of oscillation. This ordinary differential equation has an irregular singularity at 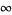 . The general solution is
. The general solution is
(2) | |||
(3) |
where the two constants 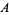 and
and 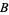 (or
(or 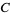 and
and 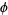 ) are determined from the initial conditions.
) are determined from the initial conditions.
Many physical systems undergoing small displacements, including any objects obeying Hooke's law, exhibit simple harmonic motion. This equation arises, for example, in the analysis of the flow of current in an electronic CL circuit (which contains a capacitor and an inductor). If a damping force such as Friction is present, an additional term 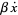 must be added to thedifferential equation and motion dies out over time.
must be added to thedifferential equation and motion dies out over time.
CITE THIS AS:
Weisstein, Eric W. "Simple Harmonic Motion." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SimpleHarmonicMotion.html

3 comments:
Harmonic oscillations are also mentioned behind the quantum world and solitons.
t'Hooft among others. colors, electroweak force?
Kay Zum Felde likes your comment very much on Facebook.
Given the speculative connections to quantum mechanics mentioned above it is natural to wonder if
this [the quantization] is related to the zero point energy of the harmonic oscillator.
Michael Aityah:
http://arxiv.org/PS_cache/arxiv/pdf/1009/1009.3176v1.pdf
Post a Comment