Saturday, January 1, 2011

General Relativity Math - for Engineers

The mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone. In relativity, on the other hand, mass, length, and the passage of time all change as an object's speed approaches the speed of light. The additional variables greatly complicates calculations of an object's motion. As a result, relativity requires the use of vectors, tensors, pseudotensors, Curvilinear coordinates and many other complex mathematical concepts.
All the mathematics discussed in this article were known before Einstein's general theory of relativity.
For an introduction based on the specific physical example of particles orbiting a large mass in circular orbits, see Newtonian motivations for general relativity for a nonrelativistic treatment and Theoretical motivation for general relativity for a fully relativistic treatment.

Contents

Vectors and Tensors

Main articles: Euclidean vector and Tensor

Vectors


Illustration of a typical vector.
In mathematics, physics, and engineering, a Euclidean vector (sometimes called a geometric[1] or spatial vector[2], or – as here – simply a vector) is a geometric object that has both a magnitude (or length) and direction. A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "one who carries".[3] The magnitude of the vector is the distance between the two points and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity.

Tensors


Stress, a second-order tensor. Stress is here shown as a series of vectors on each side of the box
A Tensor extends the concept of a vector to additional dimensions. A scalar, that is, a simple set of numbers without magnitude, would be shown on a graph as a point, a zero-dimensional object. A vector, which has a magnitude and direction, would appear on a graph as a line, which is a one-dimensional object. A tensor extends this concepts to additional dimensions. A two dimensional tensor would be called a second order tensor. This can be viewed as a set of related vectors, moving in multiple directions on a plane.

Applications

Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has both a magnitude and direction, such as velocity, the magnitude of which is speed. For example, the velocity 5 meters per second upward could be represented by the vector (0,5) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force, since it has a magnitude and direction. Vectors also describe many other physical quantities, such as displacement, acceleration, momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field.
Common applications of tensors in physics include:

Dimensions

In relativity, four-dimensional vectors, or four-vectors are required. These four dimensions are length, height, width and time. In this context, a point would be an event, as it has both a location and a time. Similar to vectors, tensors require four dimensions. One example is the Riemann curvature tensor.

 Coordinate transformation

A vector v, is shown with two coordinate grids, ex and er. In space, there is no clear coordinate grid to use. This means that the coordinate system changes based on the location and orientation of the observer. Observer ex and er in this image are facing different directions.
Here we see that ex and er see the vector differently. The direction of the vector is the same. But to ex, the vector is moving to its right. To er, the vector is moving to its left.
In physics, as well as mathematics, a vector is often identified with a tuple, or list of numbers, which depend on some auxiliary coordinate system or reference frame. When the coordinates are transformed, for example by rotation or stretching, then the components of the vector also transform. The vector itself has not changed, but the reference frame has, so the components of the vector (or measurements taken with respect to the reference frame) must change to compensate. The vector is called covariant or contravariant depending on how the transformation of the vector's components is related to the transformation of coordinates. In general, contravariant vectors are "regular vectors" with units of distance (such as a displacement) or distance times some other unit (such as velocity or acceleration); covariant vectors, on the other hand, have units of one-over-distance such as gradient. If you change units (a special case of a change of coordinates) from meters to millimeters, a scale factor of 1/1000, a displacement of 1 m becomes 1000 mm–a contravariant change in numerical value. In contrast, a gradient of 1 K/m becomes 0.001 K/mm–a covariant change in value.
The importance of coordinate transformation is because relativity states that there is no one correct reference point in the universe. On earth, we use dimensions like north, east, and elevation, which are used throughout the entire planet. There is no such system for space. Without a clear reference grid, it becomes more accurate to describe the four dimensions as towards/away, left/right, up/down and past/future. As an example event, take the signing of the Declaration of Independence. To an modern observer on Mt Rainier looking East, Revere is ahead, to the right, below, and in the past. However, to an observer in Medieval England looking North, the event is behind, to the left, neither up or down, and in the future. The event itself has not changed, the location of the observer has.

Oblique axes
Main article: Metric tensor
An oblique coordinate system is one in which the axis are not necessarily orthogonal to each other; that is, at unusual angles.

Nontensors
See also: Pseudotensor
A nontensor is a tensor-like quantity that behaves like a tensor in the raising and lowering of indices, but that does not transform like a tensor under a coordinate transformation.

Curvilinear coordinates and curved spacetime


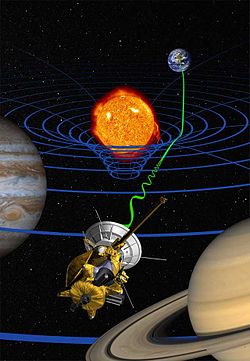
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of space and time (blue lines) due to the Sun's mass. That is, the Sun's mass causes the regular grid coordinate system (in blue) to distort and have curvature. The radio wave then follows this curvature and moves toward the Sun.
Curvilinear coordinates are coordinates in which the angles between axes can change from point-to-point. This means that rather than having a grid of straight lines, the grid instead has curvature.
A good example of this is the surface of the Earth. While maps frequently portray north, south, east and west as a simple square grid, that is not, in fact, the case. Instead, the longitude lines, running north and south, are curved, and meet at the north pole. This is because the Earth is not flat, but instead round.
In general relativity, gravity has curvature effects on the four dimensions of the universe. A common analogy is placing a heavy object on a stretched out rubber sheet which causes the rubber to bend downward. This creates a curved coordinate system around the object, much like an object in the universe creates a curved coordinate system. The mathematics here are much more complex than on Earth, as it results in four dimensions of curved coordinates instead of two as there are on Earth.

Parallel transport

Main article: Parallel transport

Example: Parallel displacement along a circle of a three-dimensional ball embedded in two dimensions. The circle of radius r is embedded in a two-dimensional space characterized by the coordinates z1 and z2. The circle itself is characterized by coordinates y1 and y2 in the two dimensional space. The circle itself is one-dimensional and can be characterized by its arc length x. The coordinate y is related to the coordinate x through the relation y1 = rcos(x / r) and y2 = rsin(x / r). This gives \partial y^1 / \partial x = - \sin( x / r) and \partial y^2 / \partial x = \cos( x / r) . In this case the metric is a scalar and is given by g = cos2(x / r) + sin2(x / r) = 1. The interval is then ds2 = gdx2 = dx2. The interval is just equal to the arc length as expected.

The interval in a high dimensional space

Imagine our four-dimensional, curved spacetime is embedded in a larger N dimensional flat space. Any true physical vector lies entirely in the curved physical space. In other words, the vector is tangent to the curved physical spacetime. It has no component normal to the four-dimensional, curved spacetime.
In the N dimensional flat space with coordinates z^n (n=1,2,3,\dots , N ) the interval between neighboring points is
ds^2_{ } = \eta_{nm} dz^n dz^m
where ηnm is the metric for the flat space. We do not assume the coordinates are orthogonal, only rectilinear.

The relation between neighboring contravariant vectors: Christoffel symbols

Main article: Christoffel symbol
The difference in 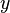y\! for two neighboring points in the surface differing by d x^{\mu}\! is
d y^{n} = {y^n}_{,\mu} d x^{\mu}
where
{y^n}_{,\mu} = {\partial y^n(x) \over \partial x^{\mu} }.
The interval between two neighboring points in physical spacetime becomes
ds^2_{ } = \eta_{nm} dy^n dy^m = \eta_{nm} {y^n}_{,\mu} {y^m}_{,\nu} dx^{\mu} dx^{\nu} = g_{\mu \nu} d x^{\mu} d x^{\nu}
where
g_{\mu \nu} = \eta_{nm} {y^n}_{,\mu} {y^m}_{,\nu}.
A contravariant vector at a point x in physical spacetime is related to the same contravariant vector at the same point y(x) in N-dimensional space by the relation
A^{n} = {y^n}_{,\mu} A^{\mu}.
The vector lies in the surface of physical spacetime.
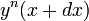Now shift the vector A^{n}\! to the point y^n(x+dx)\! keeping it parallel to itself. In other words, we hold the components of the vector constant during the shift. The vector no longer lies in the surface because of curvature of the surface.
The shifted vector can be split into two parts, one tangent to the surface and one normal to surface, as
A^{n} = A^{n}_{\mathrm{tan}} + A^{n}_{\mathrm{nor}} .
Let K^{\mu} \! be the components of A^{n}_{\mathrm{tan}} in the x coordinate system. This transformation is given by:
A^{n}_{\mathrm{tan}} = K^{\mu} {y^n}_{,\mu} (x+dx) .
The normal vector A^{n}_{\mathrm{nor}} is normal to every vector in the surface including the unit vectors that define the components of xμ. Therefore
A^{n}_{\mathrm{nor}} \; \; y_{n,\mu} (x+dx) = 0.
This allows us to write
A^{n} \; y_{n,\mu} (x+dx) = K^{\nu} g_{\mu \nu}(x+dx)
or
K_{\nu} - A_{\nu} \ \stackrel{\mathrm{def}}{=}\ \delta A_{\nu} = A^{\mu} \; {y^n}_{,\mu} y_{n,\nu, \sigma} dx^{\sigma} \ \stackrel{\mathrm{def}}{=}\ A^{\mu} \; \Gamma_{\mu \nu \sigma} dx^{\sigma}
where
\Gamma_{\mu \nu \sigma} \ \stackrel{\mathrm{def}}{=}\ {y^n}_{,\mu} y_{n,\nu, \sigma}
is a nontensor called the Christoffel symbol of the first kind. It can be shown to be related to the metric tensor through the relation
\Gamma_{\mu \nu \sigma} = {1 \over 2} \left ( g_{\mu \nu , \sigma} + g_{\mu \sigma , \nu} - g_{\nu \sigma , \mu} \right ) .
Since the Christoffel symbol can be written entirely in terms of the metric in physical spacetime, all reference to the N-dimensional space has disappeared.

Christoffel symbol of the second kind

The Christoffel symbol of the second kind is defined as
\Gamma^{\mu}_{ \nu \sigma} \ \stackrel{\mathrm{def}}{=}\ g^{\mu \lambda} \Gamma_{\lambda \nu \sigma} .
This operation is allowed for nontensors.
This allows us to write
\delta A_{\nu} = A_{\mu} \Gamma^{\mu}_{ \nu \sigma} dx^{\sigma}
and
\delta A^{\nu} = -A^{\mu} \Gamma^{\nu}_{ \mu \sigma} dx^{\sigma} .
The minus sign in the second expression can be seen from the invariance of an inner product of two vectors
\delta \left ( A^{\nu} B_{\nu} \right ) = 0 .

The constancy of the length of the parallel displaced vector

From Dirac:
The constancy of the length of the vector follows from geometrical arguments. When we split up the vector into tangential and normal parts ... the normal part is infinitesimal and is orthogonal to the tangential part. It follows that, to the first order, the length of the whole vector equals that of its tangential part.

The covariant derivative

Main article: Covariant derivative
The partial derivative of a vector with respect to a spacetime coordinate is composed of two parts, the normal partial derivative minus the change in the vector due to parallel transport
A_{\mu ; \nu} = A_{\mu , \nu} - A_{\alpha} \Gamma^{\alpha}_{ \mu \nu}.
It is relatively easy to prove that the metric tensor g_{ij}\, is covariantly constant, i.e., g_{ij;k}=0\,\ for any choice of i,j,k.
The covariant derivative of a product is
\left(A B\right)_{;\sigma}=\left(A_{;\sigma}\right )B + A\left(B_{;\sigma}\right)
that is, the covariant derivative satisfies the product rule (due to Gottfried Leibniz).

Geodesics

Main article: Geodesic
Suppose we have a point zμ that moves along a track in physical spacetime. Suppose the track is parameterized with the quantity τ. The "velocity" vector that points in the direction of motion in spacetime is
u^{\mu} = { dz^{\mu} \over d\tau }.
The variation of the velocity upon parallel displacement along the track is then
{ d u^{\nu} \over d \tau} + \Gamma^{\nu}_{\mu \sigma} u^{\mu} u^{\sigma}.
If there are no "forces" acting on the point, then the velocity is unchanged along the track and we have
{ d u^{\nu} \over d \tau} + \Gamma^{\nu}_{\mu \sigma} u^{\mu} u^{\sigma} \quad = \quad { d^2 z^{\nu} \over d \tau^2} + \Gamma^{\nu}_{\mu \sigma} { d z^{\mu} \over d \tau} { d z^{\sigma} \over d \tau} \quad = \quad 0,
which is called the geodesic equation.

Curvature tensor

Main article: Riemann curvature tensor

Definition

The curvature K of a surface is simply the angle through which a vector is turned as we take it around an infinitesimal closed path. For a two dimensional Euclidean surface we have
\delta \theta = \mbox{(Area enclosed)} \cdot K .
For a triangle on a spherical surface the angle is the excess (over 180 degrees) of the sum of the angles of the triangle. For a spherical surface of radius r, the curvature is
K = {1 \over r^2} .
The definition of curvature {R^{\beta}}_{\nu \rho \sigma} generalizes to
\delta^2 A^{\beta} = {R^{\beta}}_{\nu \rho \sigma} A^{\nu} dx^{\rho} dx^{\sigma}
where A^{\beta}\! is an arbitrary vector transported around a closed loop of area dxρdxσ along the x^{\rho}\! and x^{\sigma}\! directions.
This expression can be reduced to the commutation relation
A_{\nu ; \rho ; \sigma } - A_{\nu ; \sigma ; \rho } \ \stackrel{\mathrm{def}}{=}\ A_{\beta} {R^{\beta}}_{\nu \rho \sigma}
where
{R^{\beta}}_{\nu \rho \sigma} \ \stackrel{\mathrm{def}}{=}\ \Gamma^{\beta}_{\nu \sigma , \rho} - \Gamma^{\beta}_{\nu \rho , \sigma} + \Gamma^{\alpha}_{\nu \sigma } \Gamma^{\beta}_{\alpha \rho} - \Gamma^{\alpha}_{\nu \rho } \Gamma^{\beta}_{\alpha \sigma}.
In flat spacetime, the derivatives commute and the curvature is zero.

Symmetries of the curvature tensor

The curvature tensor is antisymmetric in the last two indices
{R^{\beta}}_{\nu\rho\sigma}=-{R^{\beta}}_{\nu\sigma\rho}.
Also
{R^{\beta}}_{\nu \rho \sigma} + {R^{\beta}}_{\rho \sigma \nu} + {R^{\beta}}_{\sigma \nu \rho } = 0
R_{\mu \nu \rho \sigma}^{ } = -R_{ \nu \mu \rho \sigma}
and
R_{\mu \nu \rho \sigma}^{ } = R_{ \rho \sigma \mu \nu } = R_{ \sigma \rho \nu \mu } .
A consequence of the symmetries is that the curvature tensor has only 20 independent components.

Bianchi identity

The following differential relation, known as the Bianchi identity is true.
{R^{\nu}}_{\mu \rho \sigma ; \tau} + {R^{\nu}}_{\mu \sigma \tau ; \rho } + {R^{\nu }}_{\mu \tau \rho ; \sigma } = 0

Ricci tensor and scalar curvature

The Ricci tensor is defined as the contraction
R_{\nu \rho} \ \stackrel{\mathrm{def}}{=}\ {R^{\mu}}_{\nu\mu \rho} .
A second contraction yields the scalar curvature
R \ \stackrel{\mathrm{def}}{=}\ g^{\nu \rho} R_{\nu \rho} = {R^{\nu}}_{\nu} .
It can be shown that consequence of the Bianchi identity is
2{R^{\alpha}}_{\sigma ; \alpha} - R_{;\sigma} = 0 .

See also

Notes

  1. ^ Ivanov 2001
  2. ^ Heinbockel 2001
  3. ^ Latin: vectus, perfect participle of vehere, "to carry"/ veho = "I carry". For historical development of the word vector, see "vector n.". Oxford English Dictionary. Oxford University Press. 2nd ed. 1989. and Jeff Miller. "Earliest Known Uses of Some of the Words of Mathematics". http://jeff560.tripod.com/v.html. Retrieved 2007-05-25. .

References

  • P. A. M. Dirac (1996). General Theory of Relativity. Princeton University Press. ISBN 0-691-01146-X. 
  • Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0. 
  • Landau, L. D. and Lifshitz, E. M. (1975). Classical Theory of Fields (Fourth Revised English Edition). Oxford: Pergamon. ISBN 0-08-018176-7. 
  • R. P. Feynman, F. B. Moringo, and W. G. Wagner (1995). Feynman Lectures on Gravitation. Addison-Wesley. ISBN 0-201-62734-5. 
  • Einstein, A. (1961). Relativity: The Special and General Theory. New York: Crown. ISBN 0-517-02961-8.
Posted by at

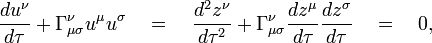
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)