Gino Fano and the Fano Plane

 The following may appear random and out-of-left field atm, but it will become important as we dig further, later, into Octonions, which like me, are non-commutative AND non-associative, seeing as how I found my lady and gave up partying many many moons ago, and loathe and despise meetings, conferences, and especially airports (and that was before 9/11).

God only a make-a so many a perfect a people. The rest-a NOT-a born Italian. Ciao bella, arividerche. Bongiorno.

Gino Fano (5 January 1871 – 8 November 1952) was an Italian mathematician. He was born in Mantua, Italy and died in Verona, Italy.
Fano worked on projective and algebraic geometry; the Fano plane, Fano fibration, Fano surface, and Fano varieties are named for him.
Ugo Fano and Robert Fano were his sons.

References

• Grattan-Guinness, Ivor (2000). The Search for Mathematical Roots 1870-1940. Princeton University Press. 

External links

• O'Connor, John J.; Robertson, Edmund F., "Gino Fano", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Fano.html .
• Gino Fano at the Mathematics Genealogy Project

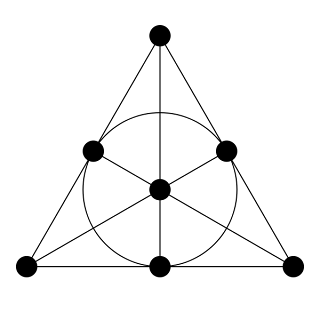
In finite geometry, the Fano plane (after Gino Fano) is the finite projective plane with the smallest possible number of points and lines: 7 each.

Contents 1 Homogeneous coordinates 2 Symmetries 3 Configurations 4 Group-theoretic construction 5 Block design theory 6 Matroid theory 7 Steiner system 8 References 9 See also

Homogeneous coordinates

The Fano plane can be constructed via linear algebra as the projective plane over the finite field with two elements. One can similarly define projective planes over any other finite field, with the Fano plane being the smallest.
Using the standard construction of projective spaces via homogeneous coordinates, the seven points of the Fano plane may be labeled with the seven non-zero ordered triples of binary digits 001, 010, 011, 100, 101, 110, and 111. This can be done in such a way that for every two points p and q, the third point on line pq has the label formed by adding the labels of p and q modulo 2. In other words, the points of the Fano plane correspond to the non-zero points of the finite vector space of dimension 3 over the finite field of order 2.
The lines of the Fano plane may also be given homogeneous coordinates, again using non-zero triples of binary digits. With this system of coordinates, a point is incident to a line if the coordinate for the point and the coordinate for the line have an even number of positions at which they both have nonzero bits: for instance, the point 101 belongs to the line 111, because they have nonzero bits at two common positions. In terms of the underlying linear algebra, a point belongs to a line if the inner product of the vectors representing the point and line is zero.
The lines can be classified into three types.

• On three of the lines the binary codes for the points have the 0 in a constant position: the line 100 (containing the points 001, 010, and 011) has 0 in the first position, and the lines 010 and 001 are formed in the same way.
• On three of the lines, two of the positions in the binary codes of each point have the same value: in the line 110 (containing the points 001, 110, and 111) the first and second positions are always equal, and the lines 101 and 011 are formed in the same way.
• In the remaining line 111 (containing the points 011, 101, and 110), each binary code has exactly two nonzero bits.

Symmetries

A permutation of the seven points of the Fano plane that carries collinear points (points on the same line) to collinear points (in other words, it "preserves collinearity") is called a "collineation", "automorphism", or "symmetry" of the plane. The full collineation group (or automorphism group, or symmetry group) is isomorphic to the projective special linear group PSL(2,7) = PSL(3,2), and the general linear group GL(3,2) (which is equal to PSL(3,2) because the field has only one nonzero element). It consists of 168 different permutations.
The automorphism group is made up of 6 conjugacy classes, which may be described in terms of their permutations of the points:

• the identity,
• 21 point permutations of type (12)(34) that keep all 3 points on one line fixed, and for one of these points, the other 2 lines through it; they interchange the other 4 points pairwise, and the other 4 lines ditto,
• 56 point permutations of type (123)(456) that rotate one triangle (a cyclic permutation of the 3 vertices, and a corresponding cyclic permutation of the 3 other points on the sides, keeping the 7th point fixed; hence "rotations about a point"); in other words: keep one point fixed, and choose 3 other points on a line, carry out a cyclic permutation of the 3 points on the line, and a corresponding cyclic permutation of the 3 other points.
• 42 point permutations of type (12)(3456) that keep one point fixed, interchange the other two points on one line through the fixed point, and perform a cyclic permutation of the remaining 4.
• two classes of point permutations of type (1234567) :
  • 24 with A mapped to B, B to C, C to the 3rd point on AB, D to 3rd point on BC, etc.
  • 24 with A mapped to B, B to C, C to the 3rd point on AC, D to 3rd point on BD, etc.

Configurations

The Fano plane contains the following numbers of configurations of points and lines of different types. For each type of configuration, the number of copies of configuration multiplied by the number of symmetries of the plane that keep the configuration unchanged is equal to 168, the size of the entire symmetry group.

• There are 7 points, and 24 symmetries fixing any point.
• There are 7 lines, and 24 symmetries fixing any line.
• There are 21 unordered pairs of points, each of which may be mapped by a symmetry onto any other unordered pair. For any unordered pair there are 8 symmetries fixing it.
• There are 21 flags consisting of a line and a point on that line. Each flag corresponds to the unordered pair of the other two points on the same line. For each flag, 8 different symmetries keep it fixed.
• There are 21 ways of selecting a quadrangle of four cyclically ordered points no three of which are collinear, and eight symmetries that fix any such quadrangle. For each flag consisting of a point p and a line l, there is a unique quadrangle in which the four points of the quadrangle are disjoint from l and the four edges of the quadrangle do not pass through p, and every quadrangle corresponds to a flag in this way.
• There are 28 triangles, which correspond one-for-one with the 28 bitangents of a quartic (Manivel 2006). For each triangle there are six symmetries fixing it, one for each permutation of the points within the triangle.
• There are 28 ways of selecting a point and a line that are not incident to each other, and six ways of permuting the Fano plane while keeping a configuration of this type fixed. For every non-incident point-line pair (p,l), the three points that are unequal to p and that do not belong to l form a triangle, and for every triangle there is a unique way of grouping the remaining four points into a non-incident point-line pair.
• There are 28 ways of specifying a hexagon in which no three consecutive vertices lie on a line, and six symmetries fixing any such hexagon.
• There are 42 ordered pairs of points, and again each may be mapped by a symmetry onto any other ordered pair. For any ordered pair there are 4 symmetries fixing it.
• There are 84 ways of specifying a triangle together with one point on that triangle, each of which has two symmetries fixing it.
• There are 84 ways of specifying a pentagon in which no three consecutive vertices lie on a line, and two symmetries fixing any pentagon.
• There are 168 different ways of specifying a triangle together with an ordering for its three points, and only the identity symmetry fixes this configuration.

Group-theoretic construction

Alternatively, the 7 points of the plane correspond to the 7 non-identity elements of the group (Z₂)³ = Z₂ × Z₂ × Z₂. The lines of the plane correspond to the subgroups of order 4, isomorphic to Z₂ × Z₂. The automorphism group of the group (Z₂)³ is that of the Fano plane, and has order 168.

Block design theory

The Fano plane is a small symmetric block design, specifically a 2-(7,3,1)-design. The points of the design are the points of the plane, and the blocks of the design are the lines of the plane. As such it is a valuable example in (block) design theory.

Matroid theory

Main article: Matroid theory

The Fano plane is one of the important examples in the structure theory of matroids. Excluding the Fano plane as a minor is necessary to characterize several important classes of matroids, such as regular, graphic, and cographic ones.

Steiner system

The Fano plane can be given the structure of a quasigroup making it a Steiner triple system. The quasigroup coincides precisely with the multiplicative structure defined by the unit octonions e₁, e₂, ..., e₇ (Baez 2002).

References

• Baez, John (2002), "The Octonions", Bull. Amer. Math. Soc. 39: 145–205, doi:10.1090/S0273-0979-01-00934-X, http://www.ams.org/bull/2002-39-02/S0273-0979-01-00934-X/home.html . Online HTML version at http://math.ucr.edu/home/baez/octonions/.
• van Lint, J.H.; Wilson, R.M. (1992), A Course in Combinatorics, Cambridge University Press, p. 197 .
• Manivel, L. (2006), "Configurations of lines and models of Lie algebras", Journal of Algebra 304 (1): 457–486, doi:10.1016/j.jalgebra.2006.04.029 .
• Weisstein, Eric W., "Fano Plane" from MathWorld.
• Finite plane and Fano plane on PlanetMath

See also

• Incidence structure
• Projective geometry
• Projective configuration
• Projective plane

Retrieved from "http://en.wikipedia.org/wiki/Fano_plane"

Categories: Projective geometry | Finite geometry | Incidence geometry | Configurations