A simple machine is a mechanical device that changes the direction or magnitude of a force.[2] In general, they can be defined as the simplest mechanisms that use mechanical advantage (also called leverage) to multiply force.[3] A simple machine uses a single applied force to do work against a single load force. Ignoring friction losses, the work done on the load is equal to the work done by the applied force. They can be used to increase the amount of the output force, at the cost of a proportional decrease in the distance moved by the load. The ratio of the output to the input force is called the mechanical advantage.
Usually the term refers to the six classical simple machines which were defined by Renaissance scientists:[4]
They are the elementary "building blocks" of which all more complicated machines (sometimes called "compound machines"[5] to emphasize that they are combinations of the simpler building blocks) are composed.[3][6] For example, wheels, levers, and pulleys are all used in the mechanism of a bicycle.
Simple machines fall into two classes; those dependent on the vector resolution of forces (inclined plane, wedge, screw) and those in which there is an equilibrium of torques (lever, pulley, wheel).
Contents |
History
The idea of a "simple machine" originated with the Greek philosopher Archimedes around the 3rd century BC, who studied the "Archimedean" simple machines: lever, pulley, and screw.[3] He discovered the principle of mechanical advantage in the lever.[7] His understanding was limited to the static balance of forces and did not include the trade-off between force and distance moved. Heron of Alexandria (ca. 10–75 AD) in his work Mechanics lists five mechanisms with which a load can be set in motion: The winch, lever, pulley, wedge, and screw.[8] During the Renaissance the classic five simple machines (excluding the wedge) began to be studied as a group. The complete dynamic theory of simple machines was worked out by Italian scientist Galileo Galilei in 1600 in Le Meccaniche ("On Mechanics"). He was the first to understand that simple machines do not create energy, only transform it.[9]Alternate definitions
Any list of simple machines is somewhat arbitrary; the central idea is that every mechanism that manipulates force should be able to be understood as a combination of devices on the list. Some variations that have been proposed to the classical list of six simple machines:- Some exclude the wedge from the list of simple machines, as it is a moving inclined plane.[3]
- The screw, being a helical inclined plane[10], is sometimes also excluded.[11] This position is less accepted because a screw converts a rotational force (torque) to a linear force.
- It has been said that the pulley, and wheel and axle can be viewed as unique forms of levers, leaving only the lever and the inclined plane as simple machines from which all others can be derived.[12][13][14][15]
- Hydraulic systems can also provide amplification of force, so some say they should be added to the list.[14][16][17]
Frictionless analysis
Although each machine works differently, the way they function is similar mathematically. In each machine, a force is applied to the device at one point, and it does work moving a load,
is applied to the device at one point, and it does work moving a load,  at another point. Although some machines only change the direction of the force, such as a stationary pulley, most machines multiply (or divide) the magnitude of the force by a factor, the mechanical advantage, that can be calculated from the machine's geometry. For example, the mechanical advantage of a lever is equal to the ratio of its lever arms.
at another point. Although some machines only change the direction of the force, such as a stationary pulley, most machines multiply (or divide) the magnitude of the force by a factor, the mechanical advantage, that can be calculated from the machine's geometry. For example, the mechanical advantage of a lever is equal to the ratio of its lever arms.Simple machines do not contain a source of energy, so they cannot do more work than they receive from the input force. When friction and elasticity are ignored, the work output (that is done on the load) is equal to the work input (from the applied force). The work is defined as the force multiplied by the distance it moves. So the applied force, times the distance the input point moves,
 , must be equal to the load force, times the distance the load moves,
, must be equal to the load force, times the distance the load moves,  [15]:
[15]:- Mechanical Advantage



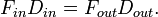
5 comments:
Hi Steven,
As you being an engineer I’m surprised you didn’t expand this to show how continuing such thoughts can lead to ideas as to how things can be strengthened as such bound up in the principle involving the moments of inertia. That is it not just being a matter of what materials we choose or the quantity of them being important, yet more so to how they may be configured as they relate to the direction of force respective to their centre of mass.
Then again perhaps you did have this in mind. That is I’m wondering if all this gaining your attention resultant of the work that Christine is putting together although one of an abstract nature as it relates to GR’s tensor considerations.
Best,
Phil
Christine is still on tensors? I wouldn't know since I've been working on The Mathematical Timeline, now complete, check it out. I'll wait till she tackles quaternions and octonions ... much more interesting to me, though I suppose it's all good.
The blog and data is excellent and informative as well.
used molding machine
This site will likely be wonderful useful resource for studying..I liked how you explained this topic.It was very well authored and easy to understand.
This rule can still be applied by workers in atlanta datacenter
This is a really informative knowledge, Thanks for posting this informative Information. Ucat practise questions
Post a Comment